题解 P1099 【树网的核】
柒葉灬
2018-08-21 09:50:14
## 思路:在直径上尺取,计算每条路径的偏心距.
- 方法1:可以选开始的一条,直接暴力计算每个点到这条点的贡献,之后进行递推,可以发现,只要两端点的改变会使得子树每个节点变化,用什么数据结构可以支持(在线修改+查询最大值)呢?——线段树!!!代码就不出示了......100多行,反正也没人看。
- 方法2:可以证明一条路径的2个端点最长距离是到直径两个端点,可以用反证法证明,所以只要处理非直径上其他点的贡献即可,预处理。
#### 整理发现,在一个线段上尺取,每一个点有一个贡献,问这些点中最大值是多少?在与两端点贡献比较,单调队列√
------------
#### 然而我们探索并没有结束,我们仔细观察,我们找的最小值肯定要么是两端点到直径端点的贡献,要么是直径上的点的贡献,那么能不能直接取最小呢?答案是可以,可以证明一条路径上,其他点的贡献<两端点到直径端点的贡献(用反证法可以证明)。
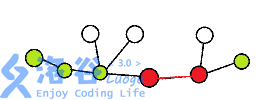
比如说染色的是直径,红色的是选的路径,显然,绿色点的贡献都小于路径俩端点的贡献,证明over!
------------
#### 即就算加上其他点的贡献,对这条路径的答案也不会有一点影响,所以单调队列就可以去掉了直接取max就行了。
```cpp
#include<cstdio>
#include<algorithm>
#define M 500005
using namespace std;
int n,m,x,y,z,k,id,top,ans=2e9;
int dis[M],fa[M],head[M];
bool mark[M];
struct edge{
int to,w,nxt;
}E[M<<1];
void add(int u,int v,int w){
E[++id]=((edge){v,w,head[u]});
head[u]=id;//存图
}
void dfs(int f,int x){
fa[x]=f;
if(dis[x]>dis[k])k=x;
for(int i=head[x];i;i=E[i].nxt){
int y=E[i].to;
if(y==f||mark[y])continue;
dis[y]=dis[x]+E[i].w;
dfs(x,y);
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<n;i++){
scanf("%d%d%d",&x,&y,&z);
add(x,y,z),add(y,x,z);
}
dis[1]=1,dfs(0,1);
dis[k]=0,dfs(0,k);
//k表示最远的端点
top=k;//找直径
for(int i=top,j=top,l=1,r=0;i;i=fa[i]){
while(dis[j]-dis[i]>m)j=fa[j];
//进行尺取,选路径。
x=max(dis[top]-dis[j],dis[i]);
//路径两端点到直径端点的最小贡献.
ans=min(ans,x);
}
for(int i=top;i;i=fa[i])mark[i]=1;
//标记直径,重新计算每个点的贡献。
for(int i=top;i;i=fa[i]){
k=i,dis[k]=0;
dfs(fa[i],i);
}
for(int i=1;i<=n;i++)
ans=max(ans,dis[i]);
//每个点的贡献,仔细想想为什么是对的。
printf("%d\n",ans);
return 0;
//去掉注释其实代码还挺短的(*^▽^*) 复杂度可以过BZOJ的数据
}
```