小学生都能看懂的错排问题解析
Planet6174
2018-08-12 22:00:56
**点赞请戳屏幕右下角粉色的圆 QwQ**
洛谷不支持 Flash 很蛋疼啊
我本来想做成交互式内容的,现在只能疯狂贴图……
---
### 你需要知道哪些信息学知识:
递推/简单DP。没了。
---
### 面向小学生的(并非严谨的)数学前置技能
1. 数集:一堆的**互不相同的**数放在一起。
2. 元素:数集中的一个数称为这个数集的一个元素。
3. 数学上的函数:$f(x)=$ 表达式
转化为信息学的写法长成这样:
```cpp
double f(double x) {
return 表达式;
}
```
4. 一一对应:通俗的说法就是一个萝卜一个坑。
数学上两个数集一一对应指的是:
有两个数集 $A$ 和 $B$,
对于 $A$ 里面任意一个数,在 $B$ 中都能找到一个数与之对应;
并且对于 $B$ 里面任意一个数,在 $A$ 中也一定能找到一个数与之对应,
那么,数集 $A$ 与数集 $B$ 一一对应。
---
### 问题
> 有 $n$ 个箱子,颜色分别为 $1\dots n$;还有 $n$ 个球,颜色也分别为 $1\dots n$。现在要将每一个球分别放入一个箱子里,并且一个箱子里只能放一个球。
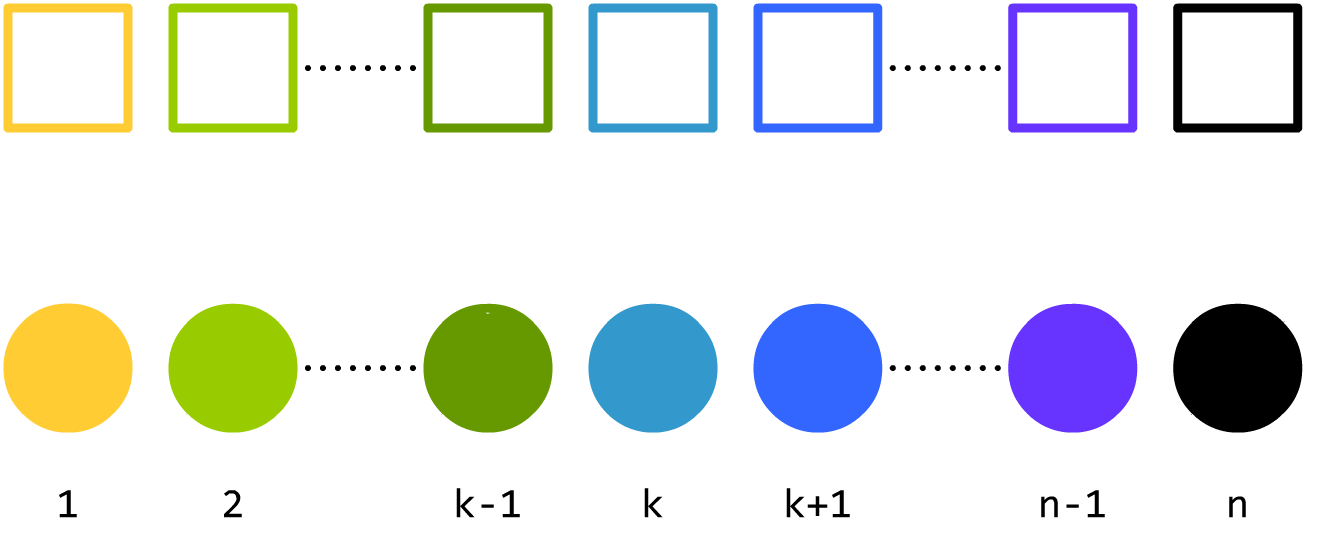
> 试求有多少种方案满足:每个箱子,和它里面球的颜色,都不一样。
> 下图使用一种不知道叫啥的线表示哪个球**不能放进**哪个箱子里(再三强调**不能放进**,有些小盆友还以为是哪个球放哪个箱子里……)。后文还会多次出现这种不知道叫啥的线。
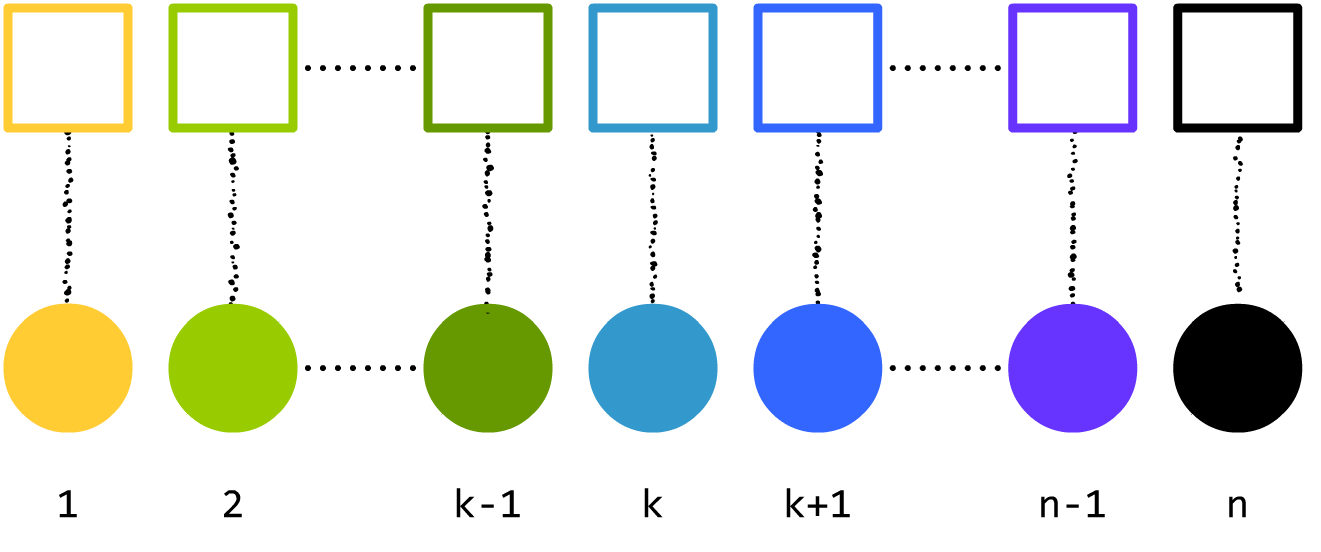
→→此处我们把 $X$ 号球 **不能放进** $Y$ 号箱称为一组**对应关系**,简写为 $X\sim Y$(注意,这不是书上正经的讲法和符号,这里这样写只是为了方便),画在图中就用这种不知道叫啥的线。←←
于是,我们换一种方式描述题目:试求有多少种方案满足:$1\sim 1$,$2\sim 2$,……,$n\sim n$。
很多人学错排问题时,就只知道上面这种形式。然而,他们没有抓住错排问题的本质。我变一下,如果 $1\sim 2$,$2\sim 3$,……,$n-1\sim n$,$n\sim 1$,答案和上面一样吗?
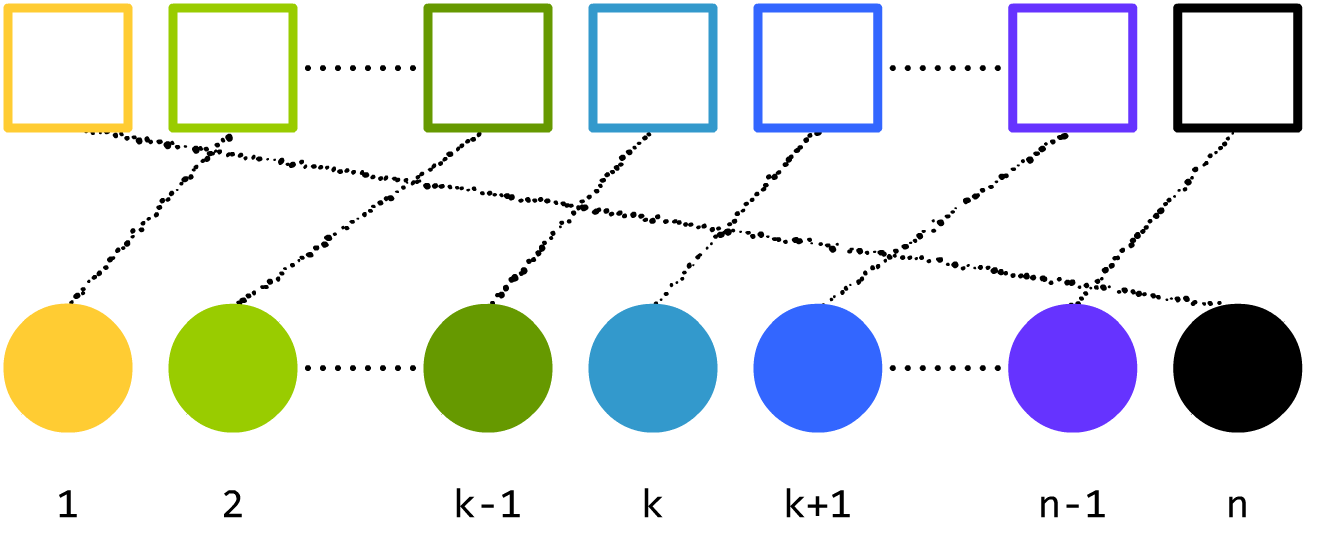
一样吧?那下面这种对应关系呢?
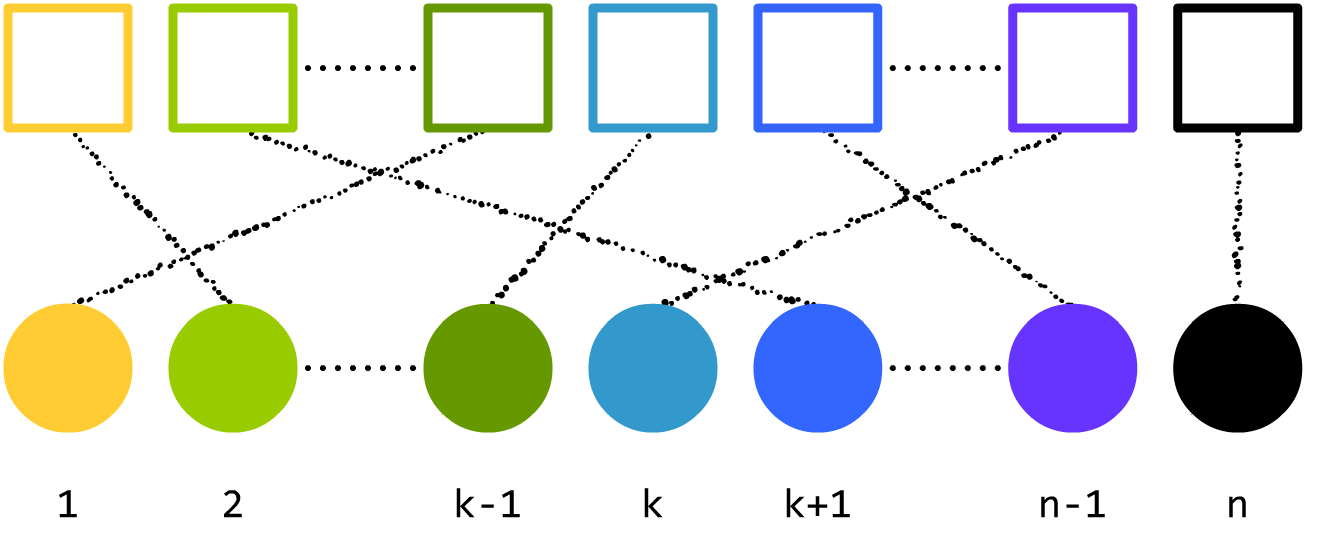
有点乱,但答案一样吧?但是,下面这几个呢?
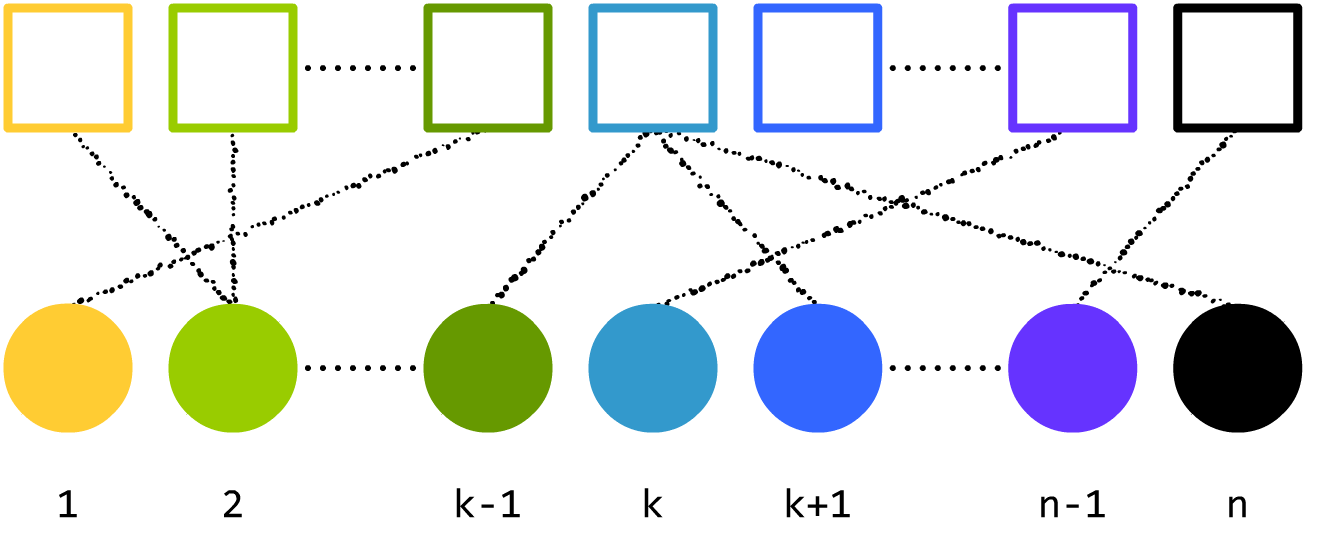
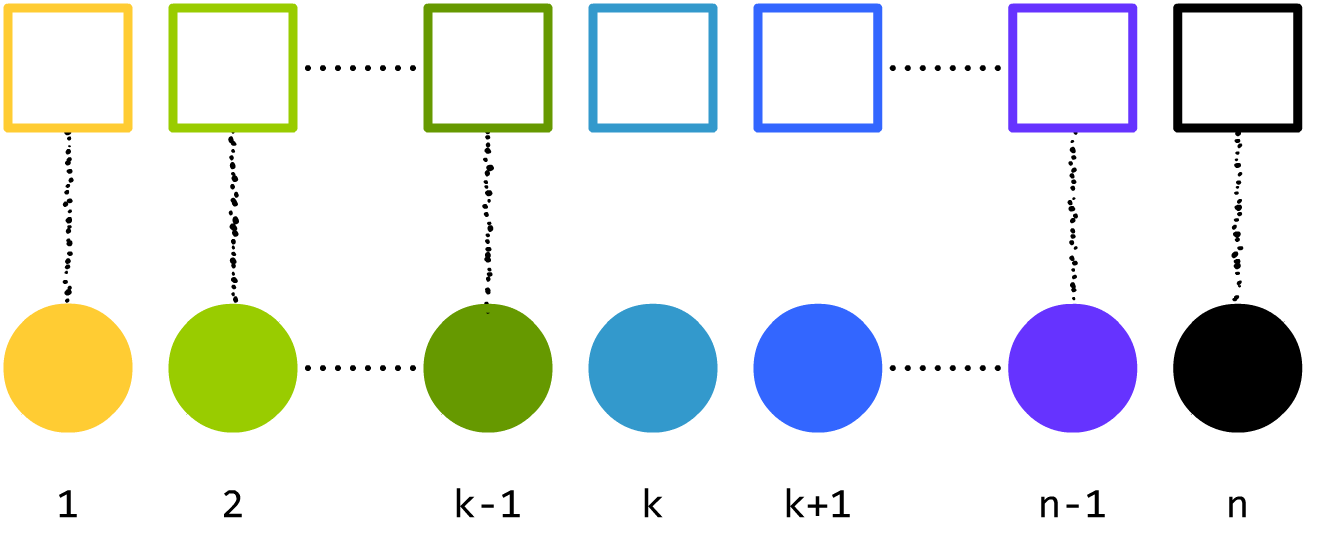
看起来不对劲。前者出现了一对多、多对一,后者出现了有些球和箱子没有对应。没错,答案会不一样。
那么,你搞清楚了正确定义了吗?
$\ $
有 $n$ 个球,$n$ 个箱子。某个箱子不能放某一个球,其他球都可以放进去;反过来,某个球一定不能放进某个箱子,并且其他箱子都允许放进去。
现在要将每个球分别放进一个箱子里,一个箱子里只能放一个球。求方案数。
$\ $
---
现在,我们进入核心部分:
### 递推式
回到开头给的题目。
数学上我们用 $D_n$ 表示有 $n$ 个球 $n$ 个箱子时的方案数。自己简单算一下可以得出 $D_1=0,$ $D_2=1,$ $D_3=2$。
我们来看下 $D_n(n\ge 4)$ 的情况。要推出怎么做,需要分类讨论。不妨分成 $n-1$ 种情况:$n$ 号球放进了 $1$ 号箱子,$n$ 号球放进了 $2$ 号箱子…… $n$ 号球放进了 $n-1$ 号箱子(现在我们在讲开头的题目,所以 $n$ 号球不能放进 $n$ 号箱子)。注意,分类讨论时要搞清楚是否涵盖了所有的情况。我们可以把所有情况列出来:
> 把 $n$ 号球放进:
> - $1$ 号箱子
> - $2$ 号箱子
> - ……
> - $(k-1)$ 号箱子
> - **$\text{k}$ 号箱子**
> - $(k+1)$ 号箱子
> - ……
> - $(n-1)$ 号箱子
现在,我们只着眼于一种情况:$n$ 号球放进了 $k$ 号箱子。
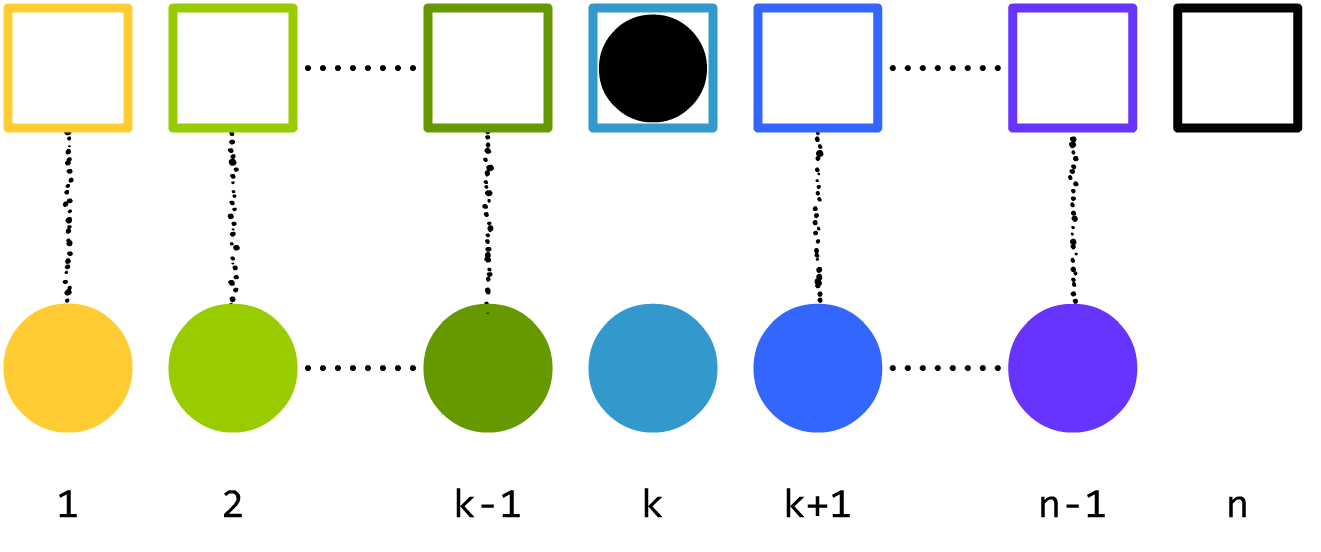
现在,我们再分为两种情况:一种是 $k$ 号球放进了 $n$ 号箱子,另一种是 $k$ 号球没有放进 $n$ 号箱子。
> 把 $n$ 号球放进:
> - $1$ 号箱子
> - $2$ 号箱子
> - ……
> - $(k-1)$ 号箱子
> - $\text{k}$ 号箱子
> * **$\text{k}$ 号球放进了 $\text{n}$ 号箱子**
> * **$\text{k}$ 号球没有放进 $\text{n}$ 号箱子**
> - $(k+1)$ 号箱子
> - ……
> - $(n-1)$ 号箱子
如果 $k$ 号球放进了 $n$ 号箱子:
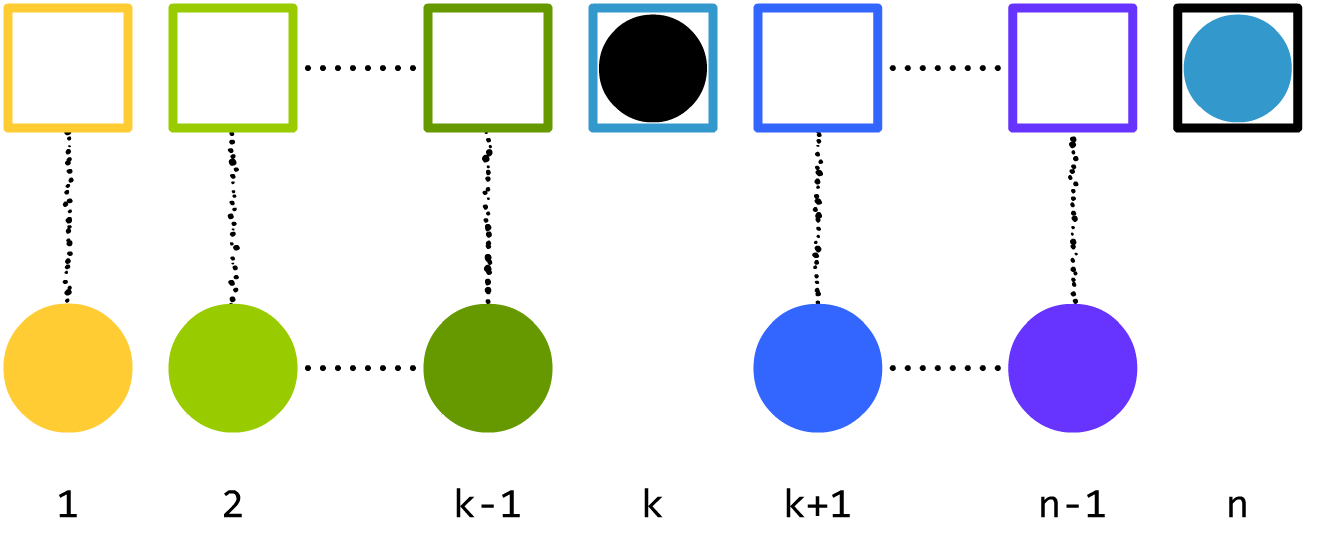
我们可以发现,如果不看 $k$ 号球 $k$ 号箱子 $n$ 号球 $n$ 号箱子,那么,将剩下的球按规定放进剩下的箱子有 $D_{n-2}$ 种方案。
> 把 $n$ 号球放进:
> - $1$ 号箱子
> - $2$ 号箱子
> - ……
> - $(k-1)$ 号箱子
> - $\text{k}$ 号箱子
> * $\text{k}$ 号球放进了 $\text{n}$ 号箱子 $\longrightarrow$ $D_{n-2}$ **种方案**
> * $\text{k}$ 号球没有放进 $\text{n}$ 号箱子
> - $(k+1)$ 号箱子
> - ……
> - $(n-1)$ 号箱子
$\ $
为了和上面区分,这里我们描述为:如果 $k$ 号球**不能**放进 $n$ 号箱子。
动脑筋想想,这个东西是不是可以写成 $k\sim n$?(回到上面读读 $\sim$ 的定义)
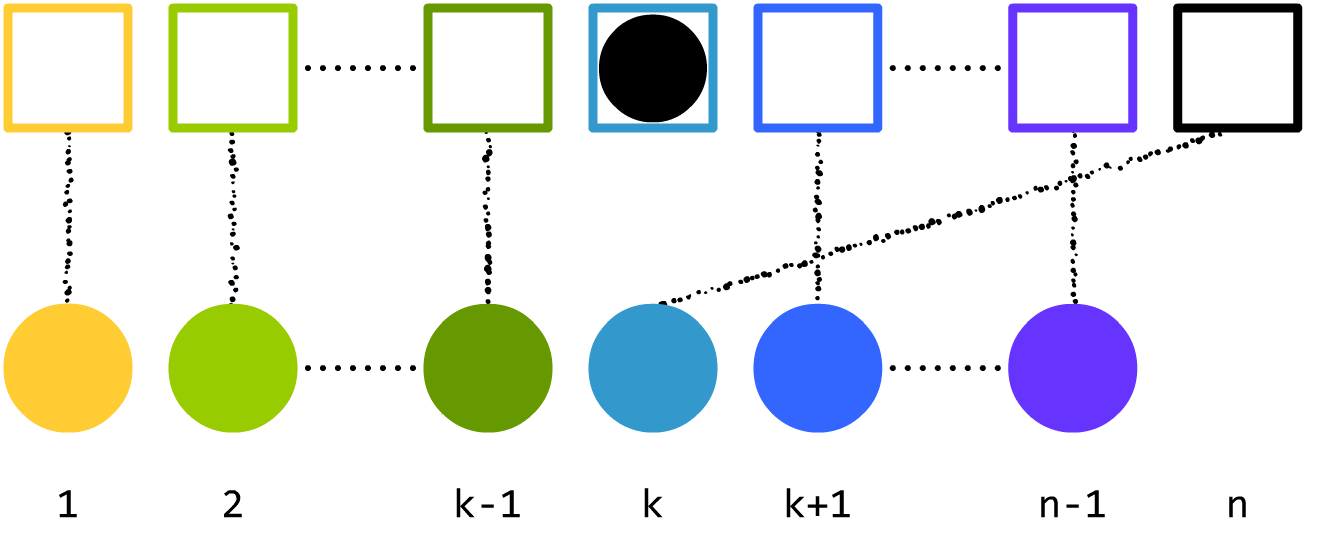
我们可以发现,如果不看 $n$ 号球和 $k$ 号箱子,那么,将剩下的球按规定放进剩下的箱子有 $D_{n-1}$ 种方案。还没看懂?那我把 $k$ 号球移过来,你能不能看懂?
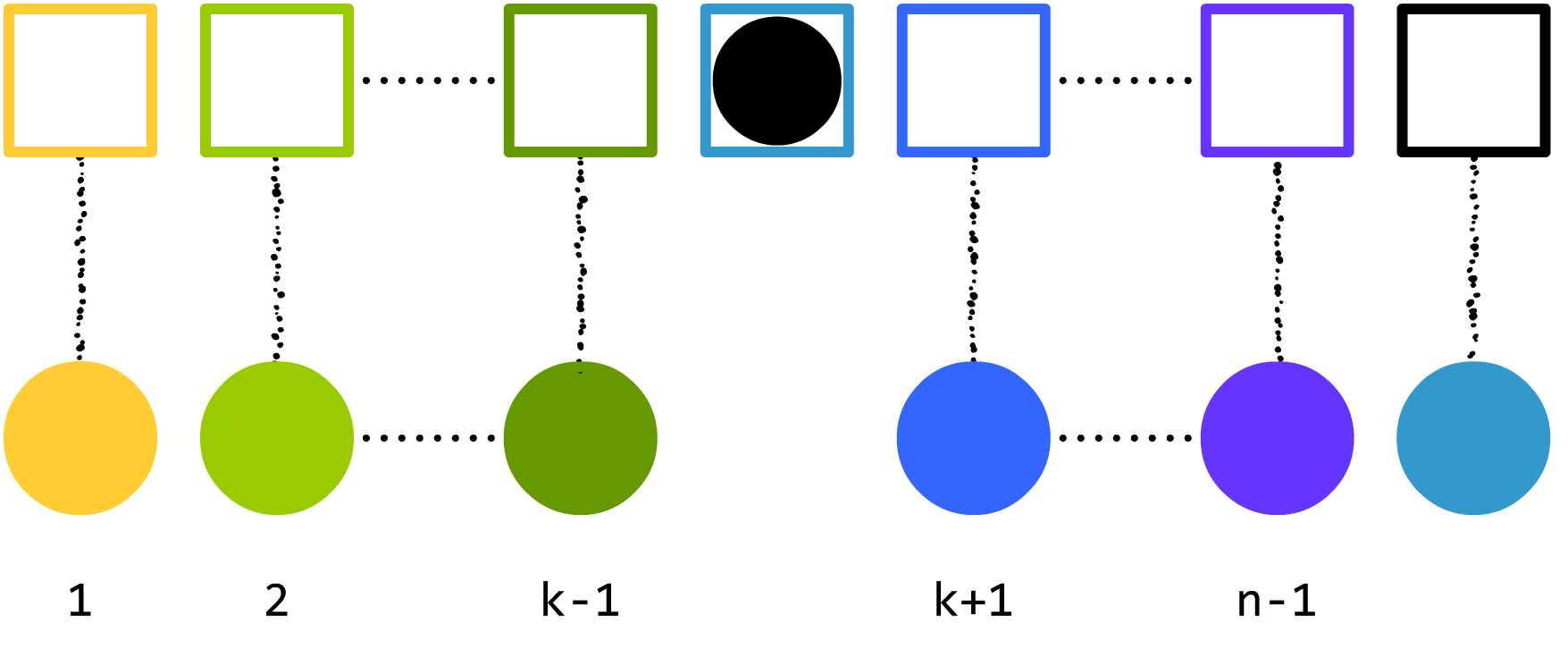
还没看懂?回到上面读读错排问题的正确定义。
> 把 $n$ 号球放进:
> - $1$ 号箱子
> - $2$ 号箱子
> - ……
> - $(k-1)$ 号箱子
> - $\text{k}$ 号箱子
> * $\text{k}$ 号球放进了 $\text{n}$ 号箱子 $\longrightarrow$ $D_{n-2}$ 种方案
> * $\text{k}$ 号球没有放进 $\text{n}$ 号箱子 $\longrightarrow$ $D_{n-1}$ **种方案**
> - $(k+1)$ 号箱子
> - ……
> - $(n-1)$ 号箱子
$\ $
我们发现,把 $n$ 号球放进 $\text{k}$ 号箱子后的两种情况我们都能够求出答案。现在,我们可以把两者合起来!
> 把 $n$ 号球放进:
> - $1$ 号箱子
> - $2$ 号箱子
> - ……
> - $(k-1)$ 号箱子
> - $\text{k}$ 号箱子 $\longrightarrow$ $D_{n-2}+D_{n-1}$ **种方案**
> * $\text{k}$ 号球放进了 $\text{n}$ 号箱子 $\longrightarrow$ $D_{n-2}$ 种方案
> * $\text{k}$ 号球没有放进 $\text{n}$ 号箱子 $\longrightarrow$ $D_{n-1}$ 种方案
> - $(k+1)$ 号箱子
> - ……
> - $(n-1)$ 号箱子
这个 $k$ 是一个未知数,也就是说,无论 $k=1$ 还是 $2$ 还是多少,答案是不变的!
> 把 $n$ 号球放进:
> - $1$ 号箱子 $\longrightarrow$ $D_{n-2}+D_{n-1}$ **种方案**
> - $2$ 号箱子 $\longrightarrow$ $D_{n-2}+D_{n-1}$ **种方案**
> - ……
> - $(k-1)$ 号箱子 $\longrightarrow$ $D_{n-2}+D_{n-1}$ **种方案**
> - $\text{k}$ 号箱子 $\longrightarrow$ $D_{n-2}+D_{n-1}$ 种方案
> - $(k+1)$ 号箱子 $\longrightarrow$ $D_{n-2}+D_{n-1}$ **种方案**
> - ……
> - $(n-1)$ 号箱子 $\longrightarrow$ $D_{n-2}+D_{n-1}$ **种方案**
最后一步,你会了吗?
$\ $
$$\large D_1=0$$
$$\large D_2=1$$
$$\large D_n=(n-1)(D_{n-1}+D_{n-2})(n\ge 2)$$
---
### 通项公式
下面这些我没有和小学生讲,错排的通项公式对小学生还是太难了一点。
$$D_n=n!\left[\frac{1}{2!}-\frac{1}{3!}+\dots+(-1)^n\frac{1}{n!}\right]$$
还有一个原因,这东西没法子快速计算……
顺便讲一下这东西怎样从递推式推导为通项公式的。以下内容来自维基。
设 $D_n = n!M_n$,则 $M_1 = 0, M_2 = \dfrac {1}{2}$。
当 $n\ge 3$ 时,$D_n = (n-1)(D_{n-1} + D_{n-2})$,即
$$n!M_{n}=(n-1)\times (n-1)!M_{n-1}+(n-1)\times (n-2)!M_{n-2}=n!M_{n-1}-(n-1)!M_{n-1}+(n-1)!M_{n-2}$$
化简得
$$nM_{n}-nM_{{n-1}}=-M_{{n-1}}+M_{{n-2}}$$
于是
$$M_{n}-M_{{n-1}}=-{\frac {1}{n}}(M_{{n-1}}-M_{{n-2}})=...=(-{\frac {1}{n}})(-{\frac {1}{n-1}})...(-{\frac {1}{3}})(M_{2}-M_{1})=(-1)^{n}{\frac {1}{n!}}$$
所以
$$\begin{aligned}M_{{n}}-M_{{n-1}}&=(-1)^{{n}}{\frac {1}{n!}}\\M_{{n-1}}-M_{{n-2}}&=(-1)^{{(n-1)}}{\frac {1}{(n-1)!}}\\\vdots \quad &=\quad \vdots \\M_{2}-M_{1}&=(-1)^{2}{\frac {1}{2!}}\\ \end{aligned}$$
将上面式子分边累加,得
$$M_{n}=(-1)^{2}{\frac {1}{2!}}+(-1)^{3}{\frac {1}{3!}}...+(-1)^{{n}}{\frac {1}{n!}}$$
因此,我们得到错排的通项公式 $$D_{n}=n!M_{n}=n!\left[{\frac {1}{2!}}-{\frac {1}{3!}}+...+(-1)^{n}{\frac {1}{n!}}\right]$$