题解 P1959 【遗址_NOI导刊2009普及(6)】
顾z
2018-09-06 10:00:03
题目描述--> [P1959 遗址_NOI导刊2009普及(6)](https://www.luogu.org/problemnew/show/P1959)
## 广告: [安利blog](https://www.luogu.org/blog/RPdreamer/#)
## 普通方法分析:
因为题目要求是**找最大正方形**~~(如果是长方形更麻烦.~~
讲真,题目不难,耗时间!
根据题目要求,我们要找的是正方形.
我们可以**根据已知两点去判断其他两点是否存在**
然后就到了~~画图课~~讲解法的时候.
下面所有的**dely代表纵坐标差值,delx代表横坐标差值.**
(记得**在输入的时候,标记圆柱坐标**.
当我们枚举的两个点所在直线平行于x轴或y轴的时候↓.
**直线两侧均可能有正方形**
(即**横坐标差值为0**或**纵坐标差值为0**的时候.)
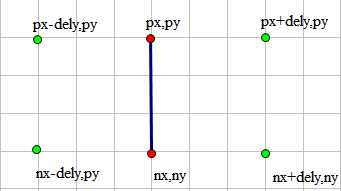
纵坐标相同的话,加减横坐标差值即可.
这时只需要**判断其他位置点是否存在**即可.
### 我们的难点在于如何判断两个点是倾斜的情况.
容易发现一个将一个倾斜正方形围起来之后,四个三角形是相等的. 像这样↓
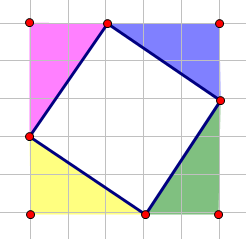
很明显全等吧!~~证明过程略~~
然后我们需要**考虑的是两个点所在直线斜率是正还是负**的问题
(亲测只考虑一种情况,不能AC此题.)
``求斜率的公式: k=Δy/Δx``
**分母不能为0!**
然后我们又开始画图 emmm
**斜率为负**有两种情况.我们可以画图如下↓
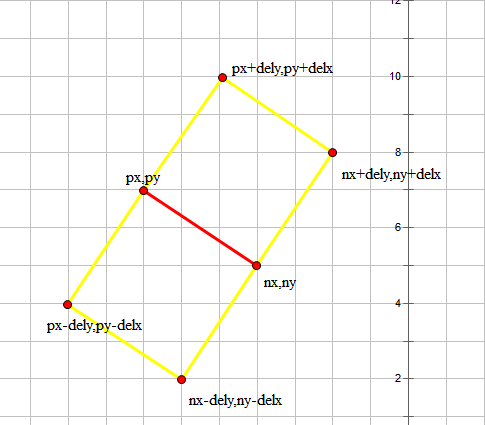
**斜率为正**.同样有两种情况如下↓
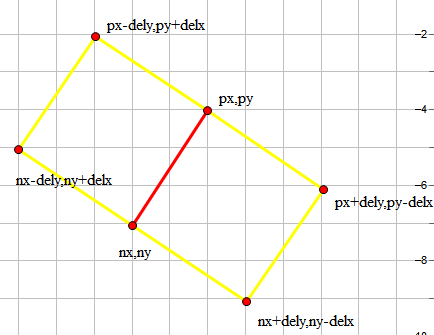
按照图片去写代码即可.
--------------------代码---------------------
```cpp
#include<bits/stdc++.h>
#define IL inline
#define RI register int
IL void in(int &x)
{
int f=1;x=0;char s=getchar();
while(s>'9' or s<'0'){if(s=='-')f=-1;s=getchar();}
while(s<='9' and s>='0'){x=x*10+s-'0';s=getchar();}
x*=f;
}
int n,x[30008],y[30008];
bool res[6008][6008];
int ans;
IL int dis(int a,int b){return abs(a-b);}
IL bool ok(int x,int y)
{
if(x<0 || y<0 || x>5000 || y>5000 || !res[x][y])return false;
return true;
}
IL void search(int px,int py,int nx,int ny)
{
int delx=dis(px,nx),dely=dis(py,ny);
if(delx==0)
{
if(ok(px+dely,py) && ok(nx+dely,ny))
ans=std::max(ans,dely*dely);
else if(ok(px-dely,py) && ok(nx-dely,ny))
ans=std::max(ans,dely*dely);
}
else if(dely==0)
{
if(ok(px,py+delx) && ok(nx,ny+delx))
ans=std::max(ans,delx*delx);
else if(ok(px,py-delx) && ok(nx,ny-delx))
ans=std::max(ans,delx*delx);
}
else if(((ny-py)/(nx-px))<0 && nx-px!=0)
{
if(ok(px+dely,py-delx) && ok(nx-dely,ny-delx))
ans=std::max(delx*delx+dely*dely,ans);
else if(ok(px+dely,py+delx) && ok(nx+dely,ny+delx))
ans=std::max(delx*delx+dely*dely,ans);
}
else if(((ny-py)/(nx-px))>0 && nx-px!=0)
{
if(ok(px+dely,py-delx) && ok(nx+dely,ny-delx))
ans=std::max(delx*delx+dely*dely,ans);
else if(ok(px-dely,py+delx) && ok(nx-dely,ny+delx))
ans=std::max(delx*delx+dely*dely,ans);
}
}
int main(void)
{
in(n);
for(RI i=1;i<=n;i++)
in(x[i]),in(y[i]),res[x[i]][y[i]]=true;
for(RI i=1;i<=n;i++)
for(RI j=1;j<=n;j++)
if(i!=j)search(x[i],y[i],x[j],y[j]);
printf("%d",ans);
}
```
如果**RE的话记得判边界**,还要**判断是否有标记**.
可能会有些麻烦,但个人感觉较好理解.
## 更简单的方法
通过我们的画图.(如果你不知道请向上看图 qwq
我们很容易发现
**新点的横坐标,只与dely有关.**
**新点的纵坐标,只与delx有关.**
**无论直线如何摆放都是如此.**
且对应坐标为一个加一个减.
因此我们可以精简代码成下面这样:
--------------------代码--------------------
```cpp
#include<bits/stdc++.h>
#define IL inline
#define RI register int
IL void in(int &x)
{
int f=1;x=0;char s=getchar();
while(s>'9' or s<'0'){if(s=='-')f=-1;s=getchar();}
while(s<='9' and s>='0'){x=x*10+s-'0';s=getchar();}
x*=f;
}
int n,x[30008],y[30008];
bool res[6008][6008];
int ans;
IL int dis(int a,int b){return abs(a-b);}
IL bool ok(int x,int y)
{
if(x<0 || y<0 || x>5000 || y>5000 || !res[x][y])return false;
return true;
}
IL void search(int px,int py,int nx,int ny)
{
int delx=dis(px,nx),dely=dis(py,ny);
if(ok(px+dely,py-delx) &&ok(nx+dely,ny-delx))
ans=std::max(ans,delx*delx+dely*dely);
else if(ok(px-dely,py+delx) && ok(nx-dely,ny+delx))
ans=std::max(ans,delx*delx+dely*dely);
//感觉少考虑了斜率为负的那一种情况,但的确是可以AC的.
/*
我们也可以加上判断斜率为负的情况.
else if(ok(px+dely,py+delx) && ok(nx+dely,ny+delx))
ans=std::max(ans,delx*delx+dely*dely);
else if(ok(px-dely,py-delx) && ok(nx-dely,ny-delx))
ans=std::max(ans,delx*delx+dely*dely);
难道数据水?
*/
}
int main(void)
{
in(n);
for(RI i=1;i<=n;i++)
in(x[i]),in(y[i]),res[x[i]][y[i]]=true;
for(RI i=1;i<=n;i++)
for(RI j=1;j<=n;j++)
if(i!=j)search(x[i],y[i],x[j],y[j]);
printf("%d",ans);
}
```
里面的``delx*delx+dely*dely`` 是**勾股定理**的内容,就不用我多说了吧.
~~**(逃**~~