题解 P4119 【[Ynoi2018]未来日记】

楼下题解写的太神了我可能没看懂…… 表示这题细节极多稍不留神就会写错 而且复杂度的分析其实也挺不对劲的…… 最后可能就是我人傻常数大吧，调了半年块长才过…… ~~管他什么题，总之lxl毒瘤数据结构天下第一~~ ________________ # 本题题解 我们先来分析一下询问会发现这是一个经典的区间kth问题 那么我们解决静态区间第k小的常用工具就是主席树(可持久化线段树)了 遗憾的是这道题有修改所以我们并不能这样做 我们的另一个思路是很自然的使用分块这个技术来维护一些关于权值的信息，结合二分答案我们可以做到$O(logn\sqrt{n})$的复杂度 这其实是一个误区,主席树之所以采取了二分的思路来解决问题是因为我们要求回答单次询问做到$O(logn)$的复杂度,这时候唯一的可行思路就是二分否则我们无法将复杂度控制在一个$log$之内 但是我们现在是使用分块解决问题,分块是有自己复杂度的就是$O(\sqrt{N})$而不是$O(logn)$这意味着分块其实和log的数据结构以及二分法并不是很搭(因为分块的结构本质上就不支持二分)如果我们我们需要强行嵌入log的数据结构的话在绝大部分情况下都会使复杂度凭空多出个log来,这在强调常数的根号算法中绝对是致命的 分块真正适合的一些更加暴力的算法,比如另一个分块 所以我们这题使用**分块套权值块状数组**这个数据结构来解决问题 具体来讲我们查询kth的时候不再二分,而是将值域分为$\sqrt{1e5}$块每块单独维护一个该值域区间里值的个数，这样的话我们查kth的时候就先for一遍每个块,将kth所在的位置定位到一段长为$\sqrt{1e5}$的值域区间里 接下来我们再挨个for这个区间里的每一个数字,看它是不是kth就可以了 这样操作的话我们查询一遍kth就是$O(\sqrt{N})$的复杂度了 那这样做有什么好处呢？ 好处就是我们无需维护值的前缀和,也就是我们无需关心"**区间里比x小的数字出现了多少次**”这个问题。 如果使用这个算法求解kth的话我们需要关心的是“**区间里x这个值出现了多少次**“以及"**区间里属于第x个值域块的数字出现了多少次**"这两个单点 的问题 那么事实上如果没有修改我们就已经可以做这道题了 我们将序列分为$\sqrt{N}$块，将值域分成$\sqrt{1e5}$块 然后记两个数组$cnt1[valid][id],cnt2[val][id]$分别表示前$id$块当中域在第$valid$个值域块的数字出现了多少次和前$id$块中$val$这个值出现了多少次 这样的话区间kth的时候我们预处理出两个$tr1[val],tr2[valid]$分别表示零散的点当中$val$这个值出现了多少次，和零散的点当中在第$valid$个值域块当中的数字出现了多少次 这样的话我们回答"**区间里属于第x个值域块的数字出现了多少次**"，这个问题的时候就两个整块的前缀和减一下然后加上零散的部分就可以回答了，同理我们也可以这样回答“**区间里x这个值出现了多少次**”这个问题 此时静态的问题我们就解决完毕了现在让我们来应对一下这个鬼畜的修改问题 首先我们已经在分块了因此我们自然会把这个修改套到分块的修改问题上去,那么分块的修改是相当套路的东西,我们暴力重构两侧的散块，然后给中间的$O(\sqrt{N})$个块打上修改标记就好了 但是问题来了这个题的标记不是一般的难打……我太笨了并不会一个严格的算法去解决这个打标记问题 所以让我们来想一个均摊复杂度是正确的算法来解决我们的修改问题 我们发现我们修改操作的一个重要的特点就是如果整个块被做了这个修改操作的话，区间中的数字种类要么-1要么不变，只有在块的一部分被做了修改操作的时候整个区间的数字种类个数才有可能+1 由于我们将序列分成$\sqrt{N}$块，显然初始每个块中数字种类不超过$O(\sqrt{N})$种,我们每次给零散的块做修改最多产生一个新的数字,因此总数字种类是$O(N+M)$级别的 那么如果我们每次在一个块的数字种类减少1(换句话讲就是合并两类数字的时候)暴力重构整个块，我们的复杂度最多是$O((N+M)\sqrt{N})$的 这样的话我们就不必担心合并两个数字的问题了因为我们可以通过暴力来解决它 现在我们只需要解决这样一个问题就是我们把一个数字变成另一种从未出现过多数字这个修改操作了，然后这个问题其实也很难做，但是我们此时已经不能通过别的巧妙的方式绕开它了……所以我们只能硬做 那么我们发现由于一定是把一种数字换成了现在未出现过的数字(但是并不是说之前没有出现过,比如说2换成3然后3换成4之后9换成3这类的逻辑关系我们都需要处理) 那么我们发现一件事无论怎么修改我们会发现一些位置的数字他们自己数值相同总是和其他位置不同的,有点像你把数组里存储的数字换了但是数组还是这个数组一样(但是把两个数字合并将会破坏这个优雅的性质，此时就可以大力重构了) 那么我们采取这样一种结构来存储所有的修改信息 我们首先记录一个$col$数组表示每个位置的数字离散化之后值+1e5的值 接下来我们记录一个$id$数组表示每个数字当前对应的值的下标 接下来我们记录一个$iv$数组表示每个下标对应的值 仅仅看这3个数组的定义没有任何意义，你也不会知道如何去使用他们 但是通过这3个数组,我们希望完成一个维护一个非常有用的恒等式那就是 **任意时刻 iv[id[col[i]]]=i这个位置的真实数字** 为了方便修改我们还需要维护这样一个恒等式就是 **任意时刻 id[col[i]]=id[i这个位置的真实数字]** **任意时刻 id[一个不存在的数字]=0** 一开始这种结构对应着下图的左半边(最底下的大圆是$col[i]$,第二层的小圆是$id[col[i]]$,第三层方框$iv[id[col[i]]]$表示这个元素的实际值  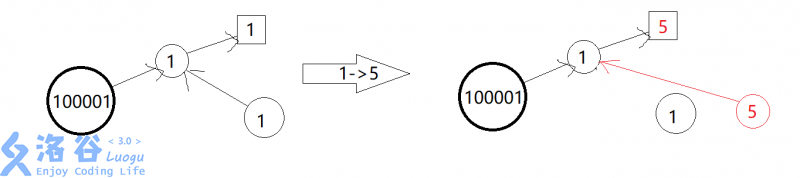接下来我们执行一个修改1->5 那么根据恒等式1我们令$iv[id[1]]=5$同时为了维护恒等式2我们令$id[5]=id[1]$，同时还是为了维护恒等式2我们令$id[1]=0$ 那么修改之后的图就是上图的右半边了,我们发现我们维护的恒等式都没有发生变化同时存储一个节点信息的方式还是和原来一样的形式 所以我们可以继续对这个结构进行修改了 然后重构之前我们先把每个位置都还原成$iv[id[col[i]]]$就可以大力重构了 这样的话我们就完成了打标记的操作了 接下来我需要修改$cnt1,cnt2$数组的值 那这个也不是很难我们统计出修改的每一块里面出现了多少个x值,然后把这些值做一个前缀和,接下来按照定义去修改$cnt1$和$cnt2$数组的值(把x那一维减去把y那一维加上对应的前缀和)就可以了 ~~一开始修改的时候写成了无脑更改后缀的导致复杂度变成了$O(N^2)$或者是$O(N^{\frac{5}{3}})$结果通过胡乱调块长和卡cache愣是过了这题~~ 然后就是注意一些细节就可以通过本题辣~ 上代码~ ```C // luogu-judger-enable-o2 #pragma GCC optimize(3) #pragma GCC optimize(Ofast) #include<cstdio> #include<algorithm> using namespace std; /**************************/ template <class T> void read(T &x){ char c; bool op = 0; while(c = getchar(), c < '0' || c > '9') if(c == '-') op = 1; x = c - '0'; while(c = getchar(), c >= '0' && c <= '9') x = x * 10 + c - '0'; if(op) x = -x; } /********************/ const int N=1e5+10;const int B=317;const int B1=350;int n;int m;int book[N];int bi1[N]; int cnb[N/B1+3][N/B+3];int sum[N][N/B+3];int bi[N];int bj[N];int tr[N];int trb[N/B1+3]; int msum[N/B+3]; int nans[N];int CNT;int trs[N]; struct block { int id[N+B];int iv[B+3];int col[B+3];int siz;int u;int ct;int rcol[B+3]; inline int& operator [](const int& x){return col[x];} inline int fd(const int& x){return iv[id[col[x]]];} inline void build()//离散化并建立标记结构 { for(int i=1;i<=siz;i++) trs[i]=book[col[i]]=(!book[col[i]])?++ct:book[col[i]]; for(int i=1;i<=siz;i++)book[col[i]]=0; for(int i=1;i<=siz;i++)iv[trs[i]]=col[i]; for(int i=1;i<=siz;i++)id[col[i]]=trs[i]; for(int i=1;i<=siz;i++)col[i]=trs[i]+100000; for(int i=1;i<=siz;i++)id[col[i]]=trs[i]; } inline void reb_md(int x,int y)//重构修改 { for(int i=1;i<=siz;i++)col[i]=iv[id[col[i]]]; for(int i=1;i<=siz;i++)col[i]=(col[i]==x)?y:col[i];ct=0;build(); } inline void reb_md(int x,int y,int l,int r) { if(sum[x][u]==sum[x][u-1])return; for(int i=1;i<=siz;i++)col[i]=iv[id[col[i]]];int cntx=0; for(int i=l;i<=r;i++)if(col[i]==x)col[i]=y,cntx++;ct=0;build(); msum[u]=cntx; } inline void lb_md(int x,int y){id[y]=id[x];iv[id[x]]=y;id[x]=0;} inline void modify(int x,int y)//根据是否需要合并两个块重构或者打标记 { if(sum[x][u]==sum[x][u-1])return; if(sum[y][u]!=sum[y][u-1])reb_md(x,y);else lb_md(x,y); msum[u]=sum[x][u]-sum[x][u-1]; } inline void deal_tr(int l,int r)//处理零散块 { for(int i=l;i<=r;i++)rcol[i]=fd(i); for(int i=l;i<=r;i++)tr[rcol[i]]++,trb[bi1[rcol[i]]]++; } inline void clear_tr(int l,int r)//清空 {for(int i=l;i<=r;i++)tr[rcol[i]]=0,trb[bi1[rcol[i]]]=0;} }bl[N/B+3]; inline int subsolve(int t1,int t2,int k)//查找kth { int ans=B1;int cnt=0;int j=1; for(cnt=cnb[j][t2]-cnb[j][t1]+trb[j];cnt<k;j++,ans=min(ans+B1,N-10),cnt+=cnb[j][t2]-cnb[j][t1]+trb[j]); for(;cnt>=k;cnt-=sum[ans][t2]-sum[ans][t1]+tr[ans],ans--);return ans+1; } inline int kth(int l,int r,int k)//分情况讨论一下就行了 { if(bi[l]==bi[r]) { bl[bi[l]].deal_tr(bj[l],bj[r]);int res=subsolve(0,0,k); bl[bi[l]].clear_tr(bj[l],bj[r]);return res; }int dl;int dr; if(bj[l]!=1){bl[bi[l]].deal_tr(bj[l],B);dl=bi[l];}else dl=bi[l]-1; if(bj[r]!=B&&r!=n){bl[bi[r]].deal_tr(1,bj[r]);dr=bi[r]-1;}else dr=bi[r]; int res=subsolve(dl,dr,k); if(bj[l]!=1){bl[bi[l]].clear_tr(bj[l],B);}if(bj[r]!=B&&r!=n){bl[bi[r]].clear_tr(1,bj[r]);} return res; } int main() { for(int i=1;i<=N-10;i++)bi[i]=(i-1)/B+1,bj[i]=(i-1)%B+1; for(int i=1;i<=N-10;i++)bi1[i]=(i-1)/B1+1;read(n);read(m); for(int i=1,v;i<=n;i++)//预处理kth表 { read(v);bl[bi[i]][bj[i]]=v; for(int j=bi[i];j<=bi[n];j++)sum[v][j]++;v=bi1[v]; for(int j=bi[i];j<=bi[n];j++)cnb[v][j]++; } for(int i=1;i<bi[n];i++)bl[i].siz=B;bl[bi[n]].siz=(n%B==0)?B:n%B; for(int i=1;i<=bi[n];i++)bl[i].u=i;for(int i=1;i<=bi[n];i++)bl[i].build(); for(int i=1,t,l,r,x,y;i<=m;i++) { read(t); if(t==1) { read(l);read(r);read(x);read(y); for(int i=bi[l];i<=bi[n];i++)msum[i]=0; if(bi[l]==bi[r]){bl[bi[l]].reb_md(x,y,bj[l],bj[r]);} else { int dl;int dr; if(bj[l]!=1)bl[bi[l]].reb_md(x,y,bj[l],B),dl=bi[l]+1;else dl=bi[l]; if(bj[r]!=B&&r!=n)bl[bi[r]].reb_md(x,y,1,bj[r]),dr=bi[r]-1;else dr=bi[r]; for(int j=dl;j<=dr;j++)bl[j].modify(x,y); }//做前缀和之后按位修改对应的表格 for(int i=bi[l]+1;i<=bi[n];i++)msum[i]+=msum[i-1]; for(int i=bi[l];i<=bi[n];i++)sum[x][i]-=msum[i]; for(int i=bi[l],bv=bi1[x];i<=bi[n];i++)cnb[bv][i]-=msum[i]; for(int i=bi[l];i<=bi[n];i++)sum[y][i]+=msum[i]; for(int i=bi[l],bv=bi1[y];i<=bi[n];i++)cnb[bv][i]+=msum[i]; }else {read(l);read(r);read(x);printf("%d\n",kth(l,r,x));} }return 0;//拜拜程序~ } ```