题解 P5280 【[ZJOI2019]线段树】

### 前言 先来扯些真实的废话。 这八成是考场上最可做的题，原因有以下： > 1. 众所周知，当九条遇上诸如斗地主、麻将、五子棋等的打完暴力直接跳过。（甚至打不出暴力） > > 2. 经回忆，往年省选最简单的题中往往都有线段树。 > > 3. 大多数毒瘤场的开题顺序都是 2、3、1。 下面，我将以我场上的心路历程，来进行本题的讲解。 --- ### 解题思路 既然每次有 $2^{x}$ 个线段树，它们 $\mathrm{modify}$ 的方式各不相同，我们就得好好盯着这个 $\mathrm{modify}$ 看，挖掘性质。 ```cpp void modify(int u, int l, int r, int pl, int pr) { if (l == pl && r == pr) { pushTag(u); return; } int mid = l + r >> 1; pushDown(u); if (pr <= mid) { modify(u << 1, l, mid, pl, pr); } else if (pl > mid) { modify(u << 1 | 1, mid + 1, r, pl, pr); } else { modify(u << 1, l, mid, pl, mid); modify(u << 1 | 1, mid + 1, r, mid + 1, pr); } } ``` 尽管线段树的结点很多，实际上，根据它们的性质分类，无非也就那么五种（认真分辨，这很重要！）： > 一类点（白色）：在 $\mathrm{modify}$ 操作中，**被半覆盖**的点。 > > 二类点（深灰）：在 $\mathrm{modify}$ 操作中，**被全覆盖**的点，并且**能被遍历到**。 > > 三类点（橙色）：在 $\mathrm{modify}$ 操作中，**未被覆盖**的点，并且**可以得到 $\mathrm{pushdown}$ 来的标记**。 > > 四类点（浅灰）：在 $\mathrm{modify}$ 操作中，**被全覆盖**的点，并且**不能被遍历到**。 > > 五类点（黄色）：在 $\mathrm{modify}$ 操作中，**未被覆盖**的点，并且**不可能得到 $\mathrm{pushdown}$ 来的标记**。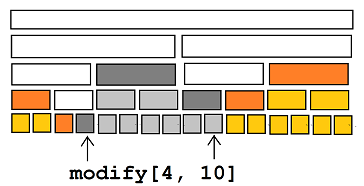  在代码中，五种点分别是这样出现的： ```cpp void modify(int u, int l, int r, int pl, int pr) { if (l == pl && r == pr) { pushTag(u); // 给二类点打标记。 // 之后的 pushdown，可能会把标记带到二类点以下的四类点去。 return; } int mid = l + r >> 1; pushDown(u); // 这里是一类点，会进行 pushdown 操作。 if (pr <= mid) { modify(u << 1, l, mid, pl, pr); // u << 1 | 1 一边就是三类点，上面的 pushdown 会传到这里。 // 之后的 pushdown，可能会把标记带到三类点以下的五类点去。 } else if (pl > mid) { modify(u << 1 | 1, mid + 1, r, pl, pr); // u << 1 一边就是三类点，上面的 pushdown 会传到这里。 // 之后的 pushdown，可能会把标记带到三类点以下的五类点去。 } else { modify(u << 1, l, mid, pl, mid); modify(u << 1 | 1, mid + 1, r, mid + 1, pr); } } ``` 类别是分得蛮清楚了，但这又有什么卵用呢？注意到同类点性质相同，倘若给它们记录 $\mathrm{dp}$ 值，它们的转移也完全相同。 没错！由于转移视类别而定，只有五种，我们可以考虑**只用一棵**线段树，然后在线段树上 $\mathrm{dp}$ ！于是最容易想到的状态定义： > 设 $f_{i,\ u}$ 为第 $i$ 次 $\mathrm{modify}$ 后，$u$ 号点在 $2^i$ 棵线段树中，多少棵被打标记。 看上去非常可做！赶紧试试五种点下的转移分别是什么？ --- #### 一类点 显然只在一类点 $\mathrm{pushdown}$，只要 $\mathrm{modify}$ ，一类点的标记就莫得存留。不 $\mathrm{modify}$ ，当然保持原状。 $$f_{i,\,u} = 0 + f_{i-1,\,u}$$ #### 二类点 只在二类点上直接打标记，所以只要 $\mathrm{modify}$ ，二类点就一定存在标记，否则保持原状。 $$f_{i,\,u} = 2^{i-1} + f_{i-1,\,u}$$ #### 三类点 不 $\mathrm{modify}$ 仍然保持，要是 $\mathrm{modify}$ ，那得通过 $\mathrm{pushdown}$ 才能让它有标记，这意味着它到根结点的一类点上，必须有至少一个原本被打标记。或者自己原本就有标记，$\mathrm{pushdown}$ 不会将其抹除。 $$f_{i,\,u} = ... + f_{i-1,\,u}$$ 哈？为什么要用 $...$？因为这次的转移有条件了，不能这么简单地用 $f$ 了！前功尽弃了吗？ --- 当然没有！办法有得是！我们不妨将需要的那个状态定义出来： > 设 $g_{i,\,u}$ 为第 $i$ 次 $\mathrm{modify}$ 后，$u$ 号点在 $2^i$ 棵线段树中，多少棵满足 $1\to u$ 上没有任何标记。 > > 反过来，满足 $1\to u$ 上至少有一个标记，就是 $2^{i} - g_{i,\,u}$ 。 这次准备挺充分了！再试试？ --- #### 一类点 同样的道理，只要 $\mathrm{modify}$ ，$1 \to u$ 的路径上的标记全部被 $\mathrm{pushdown}$ 走。 $$\begin{cases}f_{i,\,u} = 0 + f_{i-1,\,u}\\g_{i,\,u} = 2^{i-1} + g_{i-1,\,u}\end{cases}$$ #### 二类点 只要 $\mathrm{modify}$ ，$u$ 号点上一定有标记。 $$\begin{cases}f_{i,\,u} = 2^{i-1} + f_{i-1,\,u}\\g_{i,\,u} = 0 + g_{i-1,\,u}\end{cases}$$ #### 三类点 这是刚才的难点，现在有备无患了。必须 $1 \to u$ 上至少存有一个标记，才能把标记 $\mathrm{modify}$ 到三类点 $u$ 上。同理，$1 \to u$ 上没有标记，操作还是不操作，仍然不会有标记。 $$\begin{cases}f_{i,\,u} = (2^{i-1}-g_{i-1,\,u})+ f_{i-1,\,u}\\g_{i,\,u} = g_{i-1,\,u} + g_{i-1,\,u}\end{cases}$$ #### 四类点 不管是四类点还是五类点，都算是 $f$ 的盲区，既不会 $\mathrm{pushdown}$ 到，更不会像二类点直接被打上标记。所以原本有无标记，即使 $\mathrm{modify}$ ，依旧是那个样。 四类点和五类点的 $g$ 就分别跟二类点和三类点一样了，二类点的存在，使得其下属四类点在 $\mathrm{modify}$ 中不可能“门前清”。 $$\begin{cases}f_{i,\,u} = f_{i-1,\,u} + f_{i-1,\,u}\\g_{i,\,u} = 0 + g_{i-1,\,u}\end{cases}$$ #### 五类点 $$\begin{cases}f_{i,\,u} = f_{i-1,\,u} + f_{i-1,\,u}\\g_{i,\,u} = g_{i-1,\,u} + g_{i-1,\,u}\end{cases}$$ #### 边界 这总不用说了吧。 $$\begin{cases}f_{0,\,u} = 0\\g_{0,\,u} = 1\end{cases}$$ --- 这一遍下来，转移好像没啥问题了。最后是怎么实现。 每次修改暴力转移每个点绝对是不可能的。发现每次一类点、二类点、三类点只有 $O(\log n)$ 个，可以暴力，四类点、五类点有 $O(n)$ 个，然而请看它们的转移式，这显然是可以用懒标记维护的类型。 除此之外，维护 $sf_{u} = f_{u} + sf_{2u} + sf_{2u+1}$ ，即 $u$ 子树中 $f$ 的总和。易知 $sf_{1}$ 就是询问答案。 --- ### 代码实现 具体实现中可以通过把“方案数”转成“概率”从而减少一半的懒标记和常数，本人较懒，就没写了。 常见错误： > 1. 空间开小，以写法不同，四倍空间不一定足够，建议在空间方面任性一点。 > > 2. $\mathrm{pushup}$ 和 $\mathrm{pushdown}$ 不充分，多 $\mathrm{push}$ 几下不容易错。 > > 3. 转移顺序不要错，先 $f$ 后 $g$ 。 ```cpp #include <cstdio> inline int read() { char c = getchar(); int x = 0; while (c < '0' || c > '9') { c = getchar(); } while (c >= '0' && c <= '9') { x = (x << 1) + (x << 3) + (c & 15); c = getchar(); } return x; } const int N = 2000005, p = 998244353; inline int add(int x, int y) { x += y; return x >= p ? x - p : x; } inline int sub(int x, int y) { x -= y; return x >= 0 ? x : x + p; } int n, m, k = 1; struct SegmentTree { int f[N], g[N], tf[N], tg[N], sf[N]; inline void pushUp(int u) { sf[u] = add(f[u], add(sf[u << 1], sf[u << 1 | 1])); } inline void pushTf(int u, int x) { f[u] = 1ll * f[u] * x % p; tf[u] = 1ll * tf[u] * x % p; sf[u] = 1ll * sf[u] * x % p; } inline void pushTg(int u, int x) { g[u] = 1ll * g[u] * x % p; tg[u] = 1ll * tg[u] * x % p; } inline void pushDown(int u) { if (tf[u] != 1) { pushTf(u << 1, tf[u]); pushTf(u << 1 | 1, tf[u]); tf[u] = 1; } if (tg[u] != 1) { pushTg(u << 1, tg[u]); pushTg(u << 1 | 1, tg[u]); tg[u] = 1; } } void build(int u, int l, int r) { g[u] = tf[u] = tg[u] = 1; // 边界。 if (l == r) { return; } int mid = l + r >> 1; build(u << 1, l, mid); build(u << 1 | 1, mid + 1, r); } void modify(int u, int l, int r, int pl, int pr) { pushDown(u); if (l == pl && r == pr) { f[u] = add(f[u], k); // 二类点。 pushTf(u << 1, 2); pushTf(u << 1 | 1, 2); // 四类点。 } else { int mid = l + r >> 1, ul = u << 1, ur = ul | 1; g[u] = add(g[u], k); // 一类点。 if (pr <= mid) { modify(ul, l, mid, pl, pr); pushDown(ur); f[ur] = add(f[ur], sub(k, g[ur])); g[ur] = add(g[ur], g[ur]); // 三类点。 pushTf(ur << 1, 2); pushTf(ur << 1 | 1, 2); pushTg(ur << 1, 2); pushTg(ur << 1 | 1, 2); // 五类点。 pushUp(ur); } else if (pl > mid) { modify(ur, mid + 1, r, pl, pr); pushDown(ul); f[ul] = add(f[ul], sub(k, g[ul])); g[ul] = add(g[ul], g[ul]); // 三类点。 pushTf(ul << 1, 2); pushTf(ul << 1 | 1, 2); pushTg(ul << 1, 2); pushTg(ul << 1 | 1, 2); // 五类点。 pushUp(ul); } else { modify(ul, l, mid, pl, mid); modify(ur, mid + 1, r, mid + 1, pr); } } pushUp(u); } } smt; int main() { n = read(); m = read(); smt.build(1, 1, n); for (int opt, l, r; m; m--) { opt = read(); if (opt == 1) { l = read(); r = read(); smt.modify(1, 1, n, l, r); k = add(k, k); } else { printf("%d\n", smt.sf[1]); } } return 0; } ``` --- ### 尾注 这题的给点分类的思路算是比较妙的了，不少人设出了 $f$ ，却止步于想出 $g$ 的路上，这提示我们想题就要想连贯，但也不能想得太死，适当控制才有了考试的最优策略。