一模压轴题整理

# 一模压轴题整理 # 24题 ### 角等条件转化 第一题：  （2018年徐汇区一模24题） 解： (1) 由题，$C(0,3)$ $\because B(3,0)$ $\therefore b=3,k=-1$ $\therefore y=-x+3$ 设$y=x^2+bx+c$，则可得： $$\begin{cases} c=3\\ 9+3b+c=0 \end{cases}$$ $\therefore y=x^2-4x+3=(x-2)^2+1$ (2) $\therefore D(2,-1)$ 由题，$CD=2\sqrt{5},CB=3\sqrt{2},BD=\sqrt{2}$ $\therefore CB^2+BD^2=CD^2$ $\therefore \angle CBD=90^\circ$ $\therefore S_{\Delta CBD}=\frac{CB\times BD}{2}=3$ (3) 由题，$\angle CBD=45^\circ$ $\because \angle CDF=45^\circ,\angle CEB=\angle OED$ 延长$DF$交$x$轴于$G$ $\therefore \Delta CEB \sim \Delta GED$ $\therefore \frac{CE}{GE}=\frac{EB}{ED}=\frac{CB}{GD}$ 由题，$CE=\frac{3\sqrt{5}}{2},DE=\frac{\sqrt{5}}{2},EB=1.5$ $\therefore GE=2.5$ $\therefore G(-1,0)$ $\because D(2,-1)$ $\therefore F(0,-\frac{1}{3})$ 总结：本题是一个难度中等的24题，要点在于“点的坐标会说话”，关注到45度的条件，构造出相似三角形，即可解出本题。 第二题：  （2018年浦东新区一模24题） (1) 设$y=ax^2+bx+5$过$A(1,0),B(5,0)$ $$\begin{cases} a+b+5=0\\25a+5b+5=0\end{cases}$$ $$\begin{cases} a=1\\b=-6\end{cases}$$ $\therefore y=x^2-6x+5$ (2) 由题，$P(-7,-4)$ $CP=\sqrt{CA\times CB}$ 作$CH \parallel y$轴，$CI \bot AP$，垂足为$I$ 由题，$\tan \angle CAH=\frac{1}{2},\cos \angle CAH=\frac{2\sqrt{5}}{5},\sin \angle CAH=\frac{\sqrt{5}}{5}$ $\therefore CI=\frac{4\sqrt{5}}{5},AI=\frac{8\sqrt{5}}{5}$ $\therefore PI=\frac{4\sqrt{5}}{5}$ $\therefore \tan \angle CPA=\frac{CI}{PI}=\frac{\frac{4\sqrt{5}}{5} }{\frac{12\sqrt{5}}{5}}=\frac{1}{3}$ (3) 由题，$M(3,-4)$ $\therefore PM \parallel x$轴 设$\Delta AMB$高为$h$，作$BJ \bot AM$，$\therefore BJ=BM \sin M$ $\therefore \frac{1}{2} \times AB \times h = \frac{1}{2} \times AM \times BM \times \sin M$ $\therefore \sin AEM = \sin M = \frac{4}{5}$ 作$AK \bot PM$，垂足为$K$，$AK=4$ $\because \frac{AK}{AE}=\frac{4}{5}$ $\therefore E(-2,-4),E(4,-4)$ 总结：可以把角等条件转化为三角比相等，关注到三角形面积公式可以有底乘高除以二，也有夹边之积乘上夹角的正弦，进而得出三角比即可轻易解出本题。难度中等。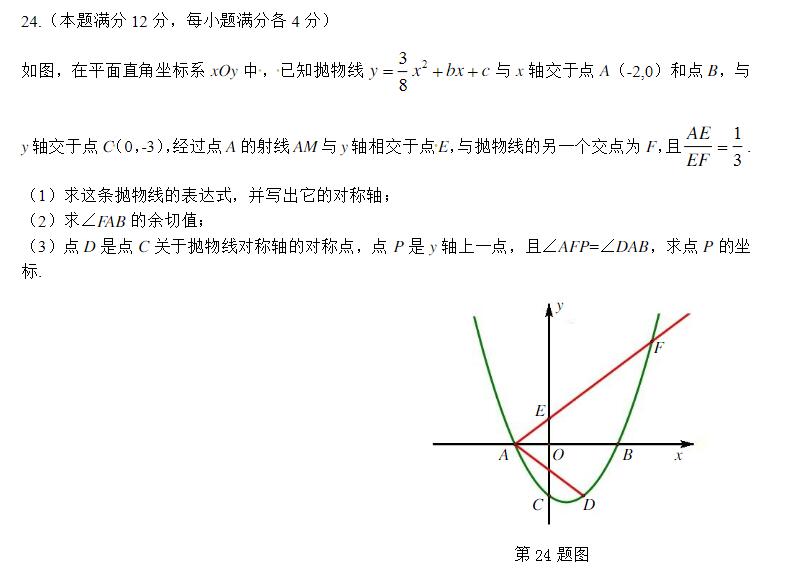 第三题：  （2018年奉贤区一模24题） (1) 将$A(-2,0)$，$C(0,-3)$代入 $$\begin{cases} \frac{3}{8} \times 4-2b+c\\c=-3\end{cases}$$ $\therefore b=-\frac{3}{4},c=-3$ $\therefore y=\frac{3}{8}x^2-\frac{3}{4}x-3$ 抛物线对称轴为直线$x=1$ (2) 作$FH \bot AB$，垂足为$H$ $\because EO \parallel FH$ $\therefore \frac{AE}{EF}=\frac{AO}{OH}$ $\therefore AH=8,OH=6$ $\therefore F(6,6)$ $\therefore \cot \angle FAB=\frac{4}{3}$ (3) 作$DI \bot AB$，垂足为$I$ 由题，$D(2,-3)$，$\cot \angle IAD=\frac{4}{3}$ $\therefore \angle FAH = \angle HAD$ $\because \angle AFP = \angle DAB$ $\therefore \angle FAH = \angle AFP$ $1^\circ PF \parallel AB$，此时$P(0,6) $2^\circ$ 设$PF$与$x$轴交于点$N(x,0)$ $\because \angle BAF = \angle AFP$ $\therefore NA=NF$ $\therefore N(\frac{17}{4},0)$ $\therefore P(0,-\frac{102}{7})$ 总结：本题要想到利用三角比相等转化为角等之后的分类讨论，难度中等偏低。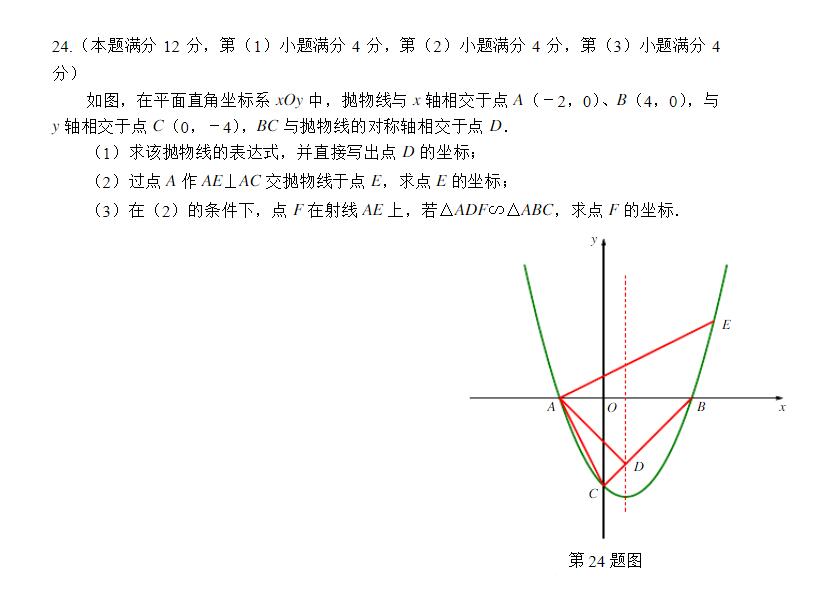 --- ### 相似的分类讨论 第一题  （2018年虹口区一模24题） (1) 设$y=a(x-2)(x-4)$，代入$C(0,-4)$可得$a=-\frac{1}{2}$ $\therefore y=\frac{1}{2}(x+2)(x-4),D(1,-3)$ (2) $\because \angle EAC = 90^\circ, \angle AOC = 90^\circ$ $\therefore \angle EAB= \angle ACO$ $\therefore \tan \angle EAB = \tan \angle ACO = \frac{1}{2}$ 作$EM \bot x$轴，垂足为$M$。设$E(x,\frac{1}{2} (x+2)(x-4))$ 则有$\frac{\frac{1}{2} (x+2)(x-4)}{x+2}=\frac{1}{2}$ $\therefore x=5$ $\therefore E(5,\frac{7}{2})$ (3) $\because OC=OB$ $\therefore \angle OBC = \angle OCB = 45^\circ$ 同理，$\angle DAB = \angle DBA = 45^\circ$ $\therefore \angle OCB= \angle DAB, \angle DAF = \angle BAC$ $\because \Delta ADF \sim \Delta ABC$ $\therefore 1^\circ \frac{AD}{CA}=\frac{AF}{CB}$ $\frac{3\sqrt{2}}{2\sqrt{5}}=\frac{AF}{4\sqrt{2}}$ $AF=\frac{12\sqrt{5}}{5}$ $F(\frac{14}{5},\frac{12}{5})$ $2^\circ \frac{AD}{CB}=\frac{AF}{CA}$ $\frac{3\sqrt{2}}{4\sqrt{2}}=\frac{AF}{2\sqrt{5}}$ $AF=\frac{3\sqrt{5}}{2}$ $F(1,\frac{3}{2})$ 总结：基础的相似分类讨论，注意抓住一个等角，然后根据SAS，用两个夹边比相等来算出AF即可。难度偏低。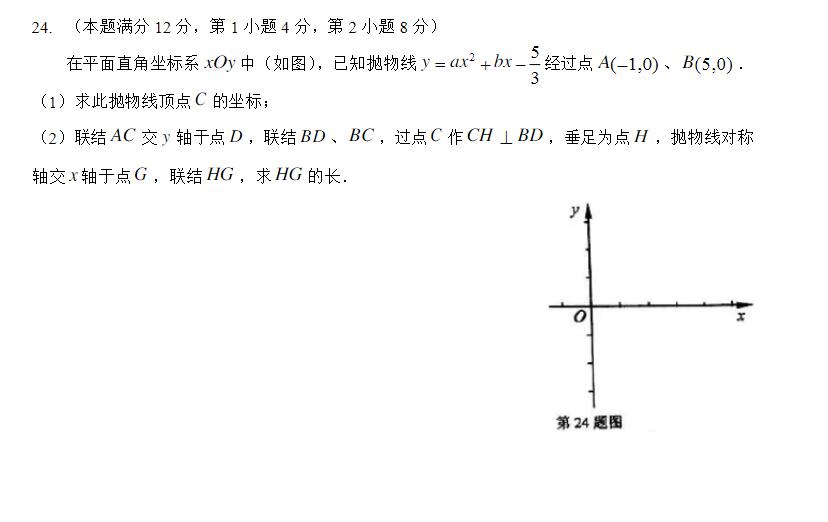 ### 其他类题目 第一题  （2018年静安区一模24题） (1) 由题，$$\begin{cases} a-b-\frac{5}{3}=0\\25a+5b-\frac{5}{3}=0\end{cases}$$ $\therefore y=\frac{1}{3}x^2-\frac{4}{3}x-\frac{5}{3}-\frac{1}{3}(x-2)^2-3$ $\therefore C(2,-3)$ (2) 由题，$D(0,-1)$ $\therefore DC=2\sqrt{2},BC=3\sqrt{2},DB=\sqrt{26}$ 由射影定理，$DH \times HB = HC^2$（附注：这里大概要证明一下，不然会扣1分，我懒得写了） 设$DH=x$，则$HB=(\sqrt{26}-x)$ $\therefore x \times (\sqrt{26}-x)=\frac{72}{13}$ $\therefore x=\frac{4\sqrt{26}}{13}$ $\therefore DH=\frac{4\sqrt{26}}{13},HB=\frac{9\sqrt{26}}{13}$ $\because DH:y=\frac{1}{5}x-1$ 设$H(x,\frac{1}{5}x-1)$ $\therefore x^2+(\frac{1}{5}x)^2=\frac{32}{13}$ $\therefore H(\frac{20}{13},-\frac{9}{13})$ $\because G(2,0)$ $\therefore HG=\frac{3\sqrt{13}}{13}$ 总结：一个不是那么常规的题目，这个题个人认为比较废原因是如上的暴力解法也可以用较小的计算量（相比暴力求解其他24题）在短时间内完成本题，而正确的做法（联结$CG$）占不到什么优势。个人认为如果用暴力做法思路很自然，难度偏易，而正确做法难度中等。