题解 P2081 【[NOI2012]迷失游乐园】

## 背景 Update2022.2.22: 纪念我的首篇题解，虽然我已经是个失败者了，但是 zcysky 成我班助了！有空更张 zcysky 照片（逃 ## 思路 ### PART I 题意：给定带权的树或基环树，从随机一点出发走**每个点至多经过一次**的路径，问期望路径长度。 $son_u$ 表示 $u$ 的子结点数量；$fa_u$ 表示 $u$ 的父结点数量，取值为 $1$ 或 $2$（因为有环）。 $down_u$ 表示从 $u$ 出发，第一步向下走的期望路径长度，「下」指子结点方向即叶子方向； $up_u$ 表示从 $u$ 出发，第一步向上走的期望路径长度，「上」指父结点方向。 > 注意：只规定了第一步向上走，第二步允许去 $u$ 的父亲 $k$ 的其他子结点。 那么从 $u$ 出发的期望路径长度为： $$\large ans_u=\dfrac{down_u\cdot son_u+up_u\cdot fa_u}{son_u+fa_u}$$ ### PART II 先考虑 50pts 的普通树做法。 $down_u$ 显然只不依赖任何的 $up$ 值： $$\large down_u=\dfrac{1}{son_u}\sum_{v\text{ is son of }u}(down_v+w_{u,v})$$ $v$ 是 $u$ 的子结点，$w_{u,v}$ 表示边权。特别的，叶子结点 $down$ 值为 $0$。 对于普通树，$u$ 至多有一个父结点 $k$，而 $up_u$ 是要依赖 $up_k,down_k$ 的： $$\large up_u=w_{u,k}+\dfrac{up_k\cdot fa_k+down_k\cdot son_k-down_u-w_{u,k}}{fa_k+son_k-1}$$ 解释如下： 不论如何，第一步贡献 $w_{u,k}$。 粗略地看，继续向上走贡献 $up_k\cdot fa_k$，转而向下走贡献 $down_k\cdot son_k$，考虑到不能走回来，故应减去 $down_u+w_{u,k}$。 第二步向上有 $fa_k$ 种选择，向下有 $son_k-1$ 种选择（不允许回来），故分母为 $fa_k+son_k-1$。 特别的，若 $k$ 仅与 $u$ 相连即 $fa_k+son_k-1=0$，则 $up_u=w_{u,k}$，没有后一项。 实现时，计算 $up,down$ 值，由于前者依赖后者，而后者不依赖前者，故流程如下： 1. 从根节点开始，递归每个子结点计算 $down$ 值； 2. 递归至 $u$ 时，先递归子结点，得到每个 $down_v$，然后计算 $down_u$，返回； 3. 得到该普通树的 $down$ 值后，从根节点的每个子结点开始，递归计算 $up$ 值； 4. 递归至 $u$ 时，根据父结点 $k$ 的信息计算 $up_u$，然后递归子结点计算，返回； 5. 根据 $up_i,down_i$ 计算 $ans_i$，最终结果为 $\displaystyle\dfrac{1}{n}\sum_{i=1}^nans_i$。 ### PART III 再来考虑基环树的情况。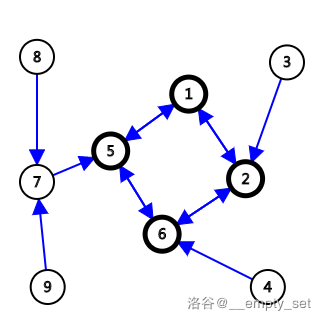  > 如图所示是一棵并不优美的基环树，箭头指向父结点（$1$ 或 $2$ 个），加粗结点是环上结点，以下简称「黑点」，其余结点简称「白点」。 我们将基环树看做**若干普通树根节点相连成环**的结果。 注意到无论从哪一点出发，第一步向下，活动范围始终在普通树内部，即：无论黑白，$down$ 值不变。 若 $u$ 是白点，只有唯一父亲 $k$，尽管此时 $fa_k$ 不一定为 $1$（白点 $u$ 的父亲 $k$ 是黑点时 $fa_k=2$），但显然考虑推导过程，$up_u$ 仍符合上文的公式。 若 $u$ 是黑点，则 $up_u$ 的计算显得和繁琐。 > $u$ 第一步去了另一个黑点，第二步可以选择继续在环上走，还可以选择钻入该黑点的子树。 为了方便处理，我们先通过深搜得到： - 黑点总数 $t$； - $\text{dfn[u]}$，维护 $u$ 是搜到的第几个黑点； - $\text{path[i]}$，维护第 $i(1\leqslant i\leqslant t)$ 个黑点的实际编号 $u(1\leqslant u\leqslant n)$； - $\text{disl[i],disr[i]}$，类似于链表的意味，维护第 $i$ 个黑点与左右相邻黑点的距离。 对于黑点 $u$，先规定第一步必须逆时针走，则有： $$\large up_u=\sum_{i}P_i\times \left(\dfrac{down_{\text{path[i]}}\cdot son_{\text{path[i]}}}{son_{\text{path[i]}}+1}+w\right)$$ 其中，$i$ 依次取 $\text{dfn[u]}+1,\text{dfn[u]}+2,\text{dfn[u]}+3,\ldots,t,1,2,3,\ldots\text{dfn[u]}-1$。 > 嗯，这个式子有失数学美感，但严谨的讲，的确是这个样子。不要紧，我们来看看这是什么意思。 根据期望的定义，期望等于**执行第 $k$ 步的概率与第 $k$ 步带来的贡献的乘积**的累加和。 先来看概率，$P_i$ 表示走到该点的概率，规定了第一步逆时针，即 $P_{\text{dfn[u]}+1}=1$。 第 $i$ 个黑点的下一个黑点是 $i\bmod t+1$，需要在第 $i$ 个黑点的 $son_{\text{path[i]}}$ 个子结点和下一个黑点之中选择下一步去哪里，那么 $P_{i\bmod t+1}=\dfrac{1}{son_{\text{path[i]}}+1}P_i$。 再来看从顺时针方向的上一个黑点走到第 $i$ 个黑点的贡献，首先有边权 $w$，即 $\text{disl[i]}$。 其次，我们需要考虑如果从此钻入第 $i$ 个黑点的子树产生的贡献，即 $\dfrac{down_{\text{path[i]}}\cdot son_{\text{path[i]}}}{son_{\text{path[i]}}+1}$。 特别的，如果第 $i$ 个黑点逆时针方向的下一个黑点就是 $u$ 的话，只能选择钻入子树而不能继续走重复的，那么分母就应该为 $son_{\text{path[i]}}$ 即钻入该子树的贡献直接就是 $down_{\text{path[i]}}$。 刚刚规定了第一步必须逆时针走，现在再规定第一步必须顺时针求一遍，最终给 $up$ 值除以 $2$ 即可。 > 当然，也可以在一开始就令 $P=\dfrac{1}{2}$，代码中也是这样实现的。 这很好理解，由于路径不重复，所以不可能顺逆时针交替，顺逆各求一遍一定包含了所有情况，只不过每个概率都放大了 $2$ 倍，现在除以 $2$ 即可。 理清逻辑关系，所有 $down$ 值只依赖其子结点的 $down$ 值，黑点的 $up$ 值依赖 $down$ 值，白点的 $up$ 值依赖黑点的 $up$ 值和 $down$ 值，故流程如下： 1. 从每个黑点即每个普通树的根节点开始，递归每个子结点计算 $down$ 值，方法同普通树； 2. 计算每个黑点的 $up$ 值，顺逆时针各求一遍，然后除以 $2$，如上文所示； 3. 从每个黑点的每个子结点开始，递归计算白点的 $up$ 值，方法同普通树； 4. 根据 $up_i,down_i$ 计算 $ans_i$，最终结果为 $\displaystyle\dfrac{1}{n}\sum_{i=1}^nans_i$。 ## 代码 > 带空格有注释，神犇请自行跳过。 实际上， $\varnothing$ 是一个蒻不禁风的被全机房吊着打的萌新，她的代码糟糕透了，特别是充实感紧凑美给人带来的视觉震撼程度都比 CK6100LGEV2 不知道差到哪里去了，她用了整整 100 行，而 CK6100LGEV2 只用了 60 行（逃）。 ```cpp #include <cstdio> const int maxn = 100005; int n, m, fa[maxn], son[maxn]; double up[maxn], down[maxn], ans; struct Edge { int to, next, w; Edge() {} Edge(int to, int next, int w): to(to), next(next), w(w) {} } e[maxn<<1]; int head[maxn], cnt; void add(int u, int v, int w) { e[++cnt] = Edge(v, head[u], w); head[u] = cnt; } #define v e[i].to int pos; bool vis[maxn], flag;//是否在环上 void dfs1(int u, int k) { vis[u] = true; for(int i = head[u]; i; i = e[i].next) if(v != k) { if(vis[v]) { pos = v; return; } dfs1(v, u); if(!flag and pos) { if(pos == u) flag = true; return; } if(flag) break; } vis[u] = false; }//将所有环上结点的 vis 标记为 true int t, disl[22], disr[22], dfn[maxn], path[22]; void dfs2(int u, int k) { dfn[u] = ++t, path[t] = u; fa[u] = 2; for(int i = head[u]; i; i = e[i].next) if(v != k and vis[v]) { if(!dfn[v]) dfs2(v, u); disr[dfn[u]] = disl[dfn[v]] = e[i].w; break; } }//处理环上信息 void dp_down(int u, int k) { for(int i = head[u]; i; i = e[i].next) if(v != k and !vis[v]) { fa[v] = 1; dp_down(v, u); son[u]++; down[u] += down[v] + e[i].w; } if(son[u]) down[u] /= son[u]; } void dp_up(int u, int k, int w) { up[u] = w; if(fa[k] + son[k] - 1) up[u] += (up[k]*fa[k]+down[k]*son[k]-down[u]-w) / (fa[k]+son[k]-1); for(int i = head[u]; i; i = e[i].next) if(v != k) dp_up(v, u, e[i].w); } void work1() { dp_down(1, 0); for(int i = head[1]; i; i = e[i].next) dp_up(v, 1, e[i].w); } double P; #define nxt(x) (x==t?1:x+1) #define pre(x) (x==1?t:x-1) void work2() { dfs1(1, 0); dfs2(pos, 0); for(int i = 1; i <= t; ++i) dp_down(path[i], 0); for(int i = 1, x; i <= t; ++i) { x = path[i]; P = 0.5; for(int j = nxt(i), y; j != i; j = nxt(j)) { y = path[j]; if(nxt(j) == i) up[x] += P * (disl[j]+down[y]); else up[x] += P * (down[y]*son[y]/(son[y]+1)+disl[j]); P /= (son[y]+1); } P = 0.5; for(int j = pre(i), y; j != i; j = pre(j)) { y = path[j]; if(pre(j) == i) up[x] += P * (disr[j]+down[y]); else up[x] += P * (down[y]*son[y]/(son[y]+1)+disr[j]); P /= (son[y]+1); } for(int j = head[x]; j; j = e[j].next) if(!vis[e[j].to]) dp_up(e[j].to, x, e[j].w); } } #undef v int main() { scanf("%d %d", &n, &m); for(int i = 1, u, v, w; i <= m; ++i) scanf("%d %d %d", &u, &v, &w), add(u, v, w), add(v, u, w); if(n != m) work1();//普通树 else work2();//基环树 for(int i = 1; i <= n; ++i) ans += (down[i]*son[i]+up[i]*fa[i]) / (son[i]+fa[i]); printf("%.5lf\n", ans / n); } ```