题解 P2516 【[HAOI2010]最长公共子序列】

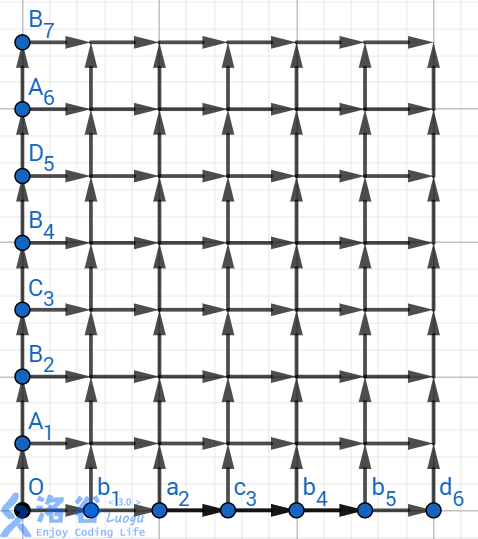
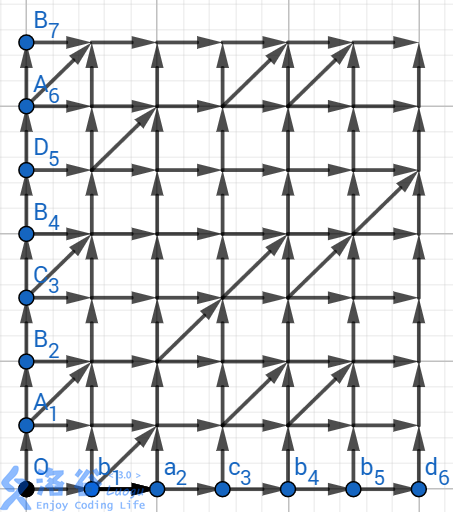
一进来就看到一个多月前秒了此题的ysn和YCB%%% 最长公共子序列的$O(n^2)$的求解，Dalao们想必都很熟悉了吧！不过蒟蒻突然发现，用网格图貌似可以很轻松地理解这个东东？ 设字符串长度为$n,m$，那么想象我们有一个$n+1$行$m+1$列的网格图，只能从左下角往右、上两个方向走。定义每条路径的长度都为$1$。记第$i$行第$j$列为$(i,j)$。 ~~话说网格图真tm难画~~  求最长公共子序列本质上是在两个序列中寻找最多的配对，而且这些配对的位置在序列中的位置也要分别递增。 那么，如果$x_i$与$y_j$相等，那么我们就从$(i-1,j-1)$向$(i,j)$连一条边。这在网格图中分明是一条条捷径，那么我们要寻找最长公共子序列，可不可以转化为寻找最短路，或者说寻找经过捷径次数最多的路径呢？  这个模型是很巧妙的，满足了配对的位置在序列中的位置分别递增（因为只能往右、上走）。 那么再看第二问。显然在这个模型中，不同的公共子序列对应的，不是至少有一条边不相同的路径，而是至少有一条**捷径**不相同的路径。那么这个该怎么DP呢？ 设到达$(i,j)$最多能经过的捷径数（即序列的两个前缀的最长公共子序列长度）为$mf_{i,j}$，方案数为$f_{i,j}$。显然$(i,j)$可以从$(i-1,j)$和$(i,j-1)$转移，如果$x_i=y_j$那么还可以从$(i-1,j-1)$转移（$mf$加上$1$）。依次转移，如果新的$mf$更大则直接覆盖原信息，如果$mf$相等则$f$相加。 然而，再次注意不同路径的定义。那么是不是可能存在这样一种情况：到$(i-1,j-1)$的一条路径，分别转移给了$(i-1,j)$和$(i,j-1)$，而再一次转移给了$(i,j)$，没有经过不同的捷径，却计算了两遍！显然只有$mf_{i-1,j-1}=mf_{i,j}$的时候上述情况才会发生，那么这时我们从$f_{i,j}$减去$f_{i-1,j-1}$即可。 思路都清晰了。在开始码DP之前，我们还需要注意这个DP的过程，每行只会从上一行转移，于是使用滚动数组优化空间，防止MLE。 ```cpp #include<bits/stdc++.h> #define RG register #define I inline #define R RG int #define G c=getchar() using namespace std; typedef long long LL; const int N=5009,YL=1e8; char x[N],y[N]; int ff[N],gg[N],mff[N],mgg[N]; int main(){ scanf("%s%s",x+1,y+1); R n=strlen(x+1)-1,m=strlen(y+1)-1,i,j,*f=ff,*g=gg,*mf=mff,*mg=mgg; g[0]=1;for(j=0;j<=m;++j)f[j]=1; for(i=1;i<=n;++i,swap(f,g),swap(mf,mg)){//滚动数组 memset(g +1,0,m<<2);//注意清空 memset(mg+1,0,m<<2); for(j=1;j<=m;++j){//三方向转移 if(x[i]==y[j])mg[j]=mf[j-1]+1,g[j]=f[j-1]; if(mf[j]>mg[j])mg[j]=mf[j],g[j]=f[j];//覆盖 else if(mf[j]==mg[j])(g[j]+=f[j])%=YL;//相加 if(mg[j-1]>mg[j])mg[j]=mg[j-1],g[j]=g[j-1]; else if(mg[j-1]==mg[j])(g[j]+=g[j-1])%=YL; if(mf[j-1]==mg[j])(g[j]+=YL-f[j-1])%=YL;//减掉重复的部分 } } printf("%d\n%d\n",mf[m],f[m]); return 0; } ```