题解 P4013 【数字梯形问题】
一扶苏一
2019-03-19 21:49:56
## Description
给定一个由 $n$ 行数字组成的数字梯形如下图所示。
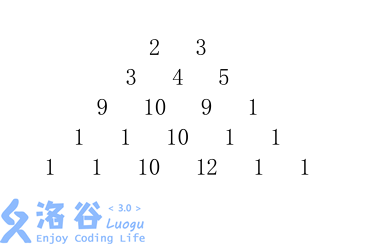
梯形的第一行有 $m$ 个数字。从梯形的顶部的 $m$ 个数字开始,在每个数字处可以沿左下或右下方向移动,形成一条从梯形的顶至底的路径。
分别遵守以下规则:
1. 从梯形的顶至底的 $m$ 条路径互不相交;
2. 从梯形的顶至底的 $m$ 条路径仅在数字结点处相交;
3. 从梯形的顶至底的 $m$ 条路径允许在数字结点相交或边相交。
## Limitation
$1~\leq~n,~m~\leq~20$
## Solution
解释一下题意,边不相交指的是不能有两条路径同时经过 $u \rightarrow~v$ 的路径。
先考虑限制 $3$,也就是没有限制的情况,做法非常显然:
> 上一层向下一层的数字连边,容量为无穷代表这条边可以走无穷次,花费为 $0$;
>
> 每个数字都拆一下点,两个点之间连边容量为无穷,代表可以选这个点无数次,花费为这个点的权值代表经过他付出的代价;
>
> $s$ 向第一层连容量为 $1$ 费用为 $0$ 的边,最后一层向 $t$ 连容量为无穷费用为 $0$ 的边,跑最大费用最大流即可。
考虑限制 $2$,一条边只能经过一次,于是将边的容量置为 $1$ 即可。
考虑限制 $1$,同理将点的容量置成 $1$ 即可。
然后如果你Wa前两个点需要注意梯形的最下面会有 $n + m$ 个点而不是 $m$ 个
## Code
```cpp
#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
#ifdef ONLINE_JUDGE
#define freopen(a, b, c)
#endif
typedef long long int ll;
namespace IPT {
const int L = 1000000;
char buf[L], *front=buf, *end=buf;
char GetChar() {
if (front == end) {
end = buf + fread(front = buf, 1, L, stdin);
if (front == end) return -1;
}
return *(front++);
}
}
template <typename T>
inline void qr(T &x) {
char ch = IPT::GetChar(), lst = ' ';
while ((ch > '9') || (ch < '0')) lst = ch, ch=IPT::GetChar();
while ((ch >= '0') && (ch <= '9')) x = (x << 1) + (x << 3) + (ch ^ 48), ch = IPT::GetChar();
if (lst == '-') x = -x;
}
namespace OPT {
char buf[120];
}
template <typename T>
inline void qw(T x, const char aft, const bool pt) {
if (x < 0) {x = -x, putchar('-');}
int top=0;
do {OPT::buf[++top] = static_cast<char>(x % 10 + '0');} while (x /= 10);
while (top) putchar(OPT::buf[top--]);
if (pt) putchar(aft);
}
const int maxn = 5010;
const int INF = 0x3f3f3f3f;
struct Edge {
int u, v, flow, fee;
Edge *nxt, *bk;
Edge(const int _u, const int _v, const int _flow, const int _fee, Edge* &h)
: u(_u), v(_v), flow(_flow), fee(_fee), nxt(h) {
h = this;
}
~Edge() {
if (this->nxt) delete this->nxt;
}
};
Edge *hd[maxn], *pre[maxn];
inline void cont(const int _u, const int _v, const int _flow, const int _fee) {
auto u = new Edge(_u, _v, _flow, _fee, hd[_u]), v = new Edge(_v, _u, 0, -_fee, hd[_v]);
(u->bk = v)->bk = u;
}
int n, m, s, t, ans;
int MU[maxn][maxn], id[maxn][maxn][2], dist[maxn], canag[maxn];
bool inq[maxn];
std::queue<int>Q;
void EK();
bool spfa();
void argu();
void setedge(int x);
void setpoint(int x);
int main() {
freopen("1.in", "r", stdin);
qr(m); qr(n);
for (int i = 1; i <= n; ++i) {
for (int j = 1, k = m + i; j < k; ++j) {
id[i][j][0] = ++t; id[i][j][1] = ++t;
qr(MU[i][j]);
}
}
s = ++t; ++t;
setpoint(1);
setedge(1);
EK();
setpoint(INF);
setedge(1);
EK();
setpoint(INF);
setedge(INF);
EK();
return 0;
}
void setpoint(int x) {
for (int i = 1; i <= t; ++i) {
delete hd[i];
hd[i] = NULL;
}
for (int i = 1; i <= m; ++i) {
cont(s, id[1][i][0], 1, 0);
}
for (int i = 1; i <= n; ++i) {
for (int j = 1, k = i + m - 1; j <= k; ++j) {
cont(id[i][j][0], id[i][j][1], x, MU[i][j]);
}
}
}
void setedge(int x) {
for (int i = 1; i < n; ++i) {
int di = i + 1;
for (int j = 1, k = i + m - 1; j <= k; ++j) {
cont(id[i][j][1], id[di][j][0], x, 0);
cont(id[i][j][1], id[di][j + 1][0], x, 0);
}
}
for (int j = 1, k = m + n - 1; j <= k; ++j) cont(id[n][j][1], t, INF, 0);
}
void EK() {
ans = 0;
while (spfa()) argu();
qw(ans, '\n', true);
}
bool spfa() {
memset(canag, 0, sizeof canag);
for (int i = 1; i <= t; ++i) dist[i] = -INF;
dist[s] = 0; Q.push(s); canag[s] = INF;
while (!Q.empty()) {
int u = Q.front(); Q.pop(); inq[u] = false;
for (auto e = hd[u]; e; e = e->nxt) if (e->flow > 0) {
int v = e->v;
if (dist[v] < (dist[u] + e->fee)) {
dist[v] = dist[u] + e->fee;
if (!inq[v]) Q.push(v);
inq[v] = true;
canag[v] = std::min(canag[u], e->flow);
pre[v] = e;
}
}
}
return dist[t] != -INF;
}
void argu() {
ans += canag[t] * dist[t];
for (auto e = pre[t]; e; e = pre[e->u]) {
e->flow -= canag[t]; e->bk->flow += canag[t];
}
}
```