P5384 【[Cnoi2019]雪松果树】

$\rm upd:$ 神仙`一扶苏一:uid65363`不仅帮我半夜交代码，还顺便帮我优化了一波，于是最终过掉了这个题，此处致以敬意。 友情提示，本篇`blog`不同于其他的题解，其渐进复杂度是最优的。 ___ **温馨提示**：以下算法思路大致相同，但是实现有不同，从$0x01$到$0x04$,共有$4$种**常数越来优秀、空间越来越优秀的写法**。 ____ ## 算法$\#\bold {0x01}$ 长链剖分 + vector离线询问 + 对dfn做前缀和 前置知识：读题 $n,q=1e6$，我会长剖！大概就是发现我们首先把询问转化到$u$的$\text {k-father}$上，然后其实就是询问以某些点为根的子树里面$dep=x$的点有多少，这东西就变成了一个经典的$dsu~on~tree$的裸题，复杂度$n\log n-n\log n$。 但实际上对于每组询问，用长剖可以实现$O(1)$求$k$级祖先，故其瓶颈在于$dsu~on~tree$太浪费时间。考虑一种在$dfn$上的算法。对于一棵$u$而言，$dfn_u$到$dfn_u+size_u-1$可以刻画整棵包含$u$在内的子树。所以考虑离线询问，直接进行前缀和，拿一个桶扫一下就做完了。时间复杂度$O(n \log n)-O(m)$，空间复杂度$O(n\log n)+O(?(n))$。其中$?(n)$可以看做一个关于$n$的超线性（与亚线性相对）函数，即给$vector$预留的空间。 码码码…码完了！submit~~发现只有$50pts$？以下是部分代码： ```cpp struct qsy{ int x, id ; bool sg ; qsy(int v, int y, int z){ x = v, id = y, sg = z ; } } ; void dfs(int u){ sz[u] = 1, dfn[++ tot] = u, Id[u] = tot ; dep[u] = L[u] = dep[fa[u][0]] + 1 ; for (int k = head[u] ; k ; k = next(k)){ dfs(to(k)) ; sz[u] += sz[to(k)] ; if (L[to(k)] > L[son[u]]) son[u] = to(k), L[u] = L[to(k)] ; } } void build(){ for (short int i = 1 ; i < 15 ; ++ i) for (int j = 1 ; j <= N ; ++ j) fa[j][i] = fa[fa[j][i - 1]][i - 1] ; } void dfs(int u, int tp){ top[u] = tp, L[u] = L[u] - dep[tp] + 1 ; if (son[u]) dfs(son[u], tp) ; for (int k = head[u] ; k ; k = next(k)) if (to(k) != son[u]) dfs(to(k), to(k)) ; } int query(int u, int k){ if (!k) return u ; if (k > dep[u]) return 0 ; u = fa[u][hb[k]] ; k ^= 1 << hb[k] ; if (!k) return u ; if (dep[u] - dep[top[u]] == k) return top[u] ; int dif = dep[u] - dep[top[u]] ; if (dep[u] - dep[top[u]] > k) return _down[top[u]][dif - k - 1] ; return _up[top[u]][k - dif - 1] ; } function :main{ for (i = 2 ; i <= N ; ++ i) u = qr(), add(i, u) ; dfs(1, 0), dfs(1, 0, 1), build() ; for (i = 1 ; i <= N ; ++ i) if (i >> hm & 1) hb[i] = hm ++ ; else hb[i] = hm - 1 ; for (i = 1 ; i <= N ; ++ i){ if (top[i] != i) continue ; l = 0, u = i ; while (l < L[i] && u) u = fa[u][0], ++ l, _up[i].pb(u) ; l = 0, u = i ; while (l < L[i] && u) u = son[u], ++ l, _down[i].pb(u) ; } for (i = 1 ; i <= M ; ++ i){ u = qr(), k = qr(), v = query(u, k) ; if (!v) continue ; q[Id[v]].pb(qsy(dep[v] + k, i, -1)), q[Id[v] + sz[v] - 1].pb(qsy(dep[v] + k, i, 1)) ; } for (i = 1 ; i <= N ; ++ i){ buc[dep[dfn[i]]] ++ ; for (j = 0 ; j < q[i].size() ; ++ j) ans[q[i][j].id] += buc[q[i][j].x] * q[i][j].sg ; } } ``` 是的，本题空间$\rm 128Mb$，$O(n\log n)+O(?(n))$的空间**不可承受**，因为实践中会发现$O(n\log n)\leq O(?(n))$，也就是说大头在vector…… 但其实vector并不是很好优化，因为询问是要离线的。于是考虑换个空间开销小的与预处理方式—— ## 算法$\#\bold {0x02}$ 栈 + vector离线询问 + 对dfn做前缀和 然后发现，其实如果不强制在线，直接用栈做$k$级祖先是一个经典问题~~nmd哪来那么多经典问题~~。就是类似用栈模仿递归的做法： ```cpp int stk[MAXN], top ; void do_do(const int &u){ stk[++ top] = u ; for (register int i = 0 ; i < pq[u].size() ; ++ i){ register int op = pq[u][i].id ; v[op] = (top > kk[op]) ? stk[top - kk[op]] : 0 ; } for (register int k = head[u] ; k ; k = next(k)) do_do(to(k)) ; -- top ; } function :main{ for (i = 1 ; i <= M ; ++ i) uu[i] = qr(), kk[i] = qr(), pq[uu[i]].pb(qsx(kk[i], i)) ; } ``` 然后就有了一个时间复杂度$O(n)-O(n)$，空间复杂度$O(?(n))$的做法，需要多用到一个vector。之后就会发现……它喜提了$\mathsf {MLE}$，不过分数变成了$70pts$。考虑问题所在，还是vector太慢了，于是插播一个细节，就是中途我花了一些时间学习了一下怎么清空vector的内存，大概是这样： ```cpp template < class T > il void _clean( vector< T >& vt ) { vector <T> vtTemp ; vtTemp.swap(vt) ; } function :main{ do_do(1) ; for (i = 1 ; i <= N ; ++ i) if (pq[i].size()) _clean(pq[i]) ; } ``` 喜闻乐见的是终于不卡空间了，但是却毫无征兆地$\mathscr{TLE}$了。不过想想也自然，这其实就相当于声明$1,000,000$个$vector$，算导上写过，这种动态表一般都是`低于1/4重构`或者`倍增式重构`，常数可想而知。 并且$vector$具有两种属性，$\rm vec.capacity()$和$\rm vec.size()$，前者是向内存申请的空间，后者是实际使用的空间，一般情况下$\rm capacity$会严格大于$\rm size$。同时有三种成员函数用来清零，`resize(n)`同时释放两者，`reserve(n)`只会释放$\rm capacity$，$\rm clear()$只会清空$\rm size$。 但最后，Luogu评测机的特性导致实际应用中这几个没有什么bird区别，于是还是选了最快的$\rm clear$。喜提$70pts$. 然后最让人心累的来了： ## 算法$\#\bold {0x03}$ 算法2 + 各种奇怪的技巧 + 对询问直接分配内存 分为两个$part$，$part·1$我$11.3$写了一下午+半晚上，$part·2$我$11.4$又写了一下午。 ### $\rm Part · 1$ 奇怪的技巧 首先就是考虑如何回收那些不需要用的数组，能少$1e6$是$1e6$啊，大概思想就是vector回收+数组重复使用，并且尽量使用不需要`memset`就可以清空的数组，效果：依然$70pts$，但是空间下降至$110 ± 7$左右。 于是发现空间可控之后，就可以上一个毒瘤东西——$fread$. 不过这东西是真的有效（但仅限于本OJ某些时段，比如下午3点以后到晚上11点之前），很轻松的让我获得了$95pts$的高分……但是问题就在于，$fread$的$\rm ch\_top$这边量的大小，一般都是$1e7$级别，大了就$\mathsf{MLE}$，小了会导致$\mathsf{WA}$，只能在一定区间内波动——而波动的不只是自己敲下的数字，还有评测机。。。于是就会出现交$50$余份只调整了一些参数的代码，会出现在$70pts$~$95pts$激烈波动的情况…… 不说了，fread葬送青春。于是这一个$part$最终的代码长这样： ```cpp #include <bits/stdc++.h> #pragma GCC target("avx") #pragma GCC optimize(2) #pragma GCC optimize(3) #pragma GCC optimize("Ofast") const int ch_top = 22000001 ; char ch[ch_top],*now_r=ch-1,*now_w=ch-1; il int read(){ while (*++now_r < 48) ; register int x = *now_r - 48 ; while (*++now_r >= 48) x = (x << 1) + (x << 3) + *now_r - 48 ; return x ; } il void write(int x){ static char st[7] ; static int top ; while (st[++ top] = 48 + x % 10, x /= 10) ; while (*++ now_w = st[top], -- top) ; *++ now_w = ' ' ; } il void add(const int &u, const int &v){ E[++ cnt].to = u, E[cnt].next = head[v], head[v] = cnt ; } function :main(){ fread(ch, 1, ch_top, stdin) ; fwrite(ch,1,now_w-ch,stdout) ; return 0 ; } ``` ps：没有展现出来数组混用，大概就是边表里面的$head$数组被我用来当做ans数组了这种感觉的一系列操作。 ### $\rm Part · 2$ 手动分配内存 起因大概是这样： > uoj群 > > 我：有没有什么减少vector占内存的方法？ > > 神仙1：强行resize？或者先算好每个vector要多大，然后resize之后当数组用？ > > 神仙2： 如果我知道多大我为什么不开一个大数组然后分配指针（ 一语点醒梦中人.wtcl 然后我就~~开始学习内存分配~~换了个写法，大体就是把$vector$都成了指针，每次手动`new`出需要多少空间，我想这样怎么说也不会被卡了吧……结果MLE，于是还是只能手动`delete`.这一部分代码大概长这样： ```cpp struct qsy{ int x, id ; bool sg ; } ; int *p[MAXN] ; qsy *q[MAXN] ; int main(){ N = qr(), M = qr() ; rg int u, op ; dep[1] = 1 ; for (rg int i = 2, j ; i <= N ; ++ i) j = qr(), to(++ cnt) = i, next(cnt) = head[j], head[j] = cnt ; cnt = 0, dfs(1) ; for (rg int i = 1 ; i <= M ; ++ i) v[i] = qr(), kk[i] = qr(), buc[v[i]] ++ ; for (rg int i = 1 ; i <= N ; ++ i) p[i] = new int[buc[i] + 1], p[i][0] = buc[i] = 0 ; for (rg int i = 1 ; i <= M ; ++ i) p[v[i]][++ p[v[i]][0]] = i, v[i] = 0 ; cnt = 0, do_do(1) ; for (rg int i = 1 ; i <= N ; ++ i) delete p[i] ; for (rg int i = 1 ; i <= M ; ++ i) buc[Id[v[i]]] ++, buc[Id[v[i]] + sz[v[i]] - 1] ++ ; for (rg int i = 0 ; i <= N ; ++ i) q[i] = new qsy[buc[i] + 1], q[i][0].x = buc[i] = 0 ; for (rg int i = 1, j ; i <= M ; ++ i) { if (!v[i]) continue ; u = Id[v[i]], j = dep[v[i]] + kk[i], op = u + sz[v[i]] - 1 ; q[u][++ q[u][0].x] = (qsy){j, i, 0}, q[op][++ q[op][0].x] = (qsy){j, i, 1} ; } for (rg int i = 1 ; i <= N ; ++ i){ buc[dep[dfn[i]]] ++ ; for (rg int j = 1 ; j <= q[i][0].x ; ++ j) head[q[i][j].id] += q[i][j].sg ? buc[q[i][j].x] : -buc[q[i][j].x] ; } for (rg int i = 1 ; i <= M ; ++ i) printf("%d ", head[i] > 0 ? head[i] - 1 : head[i]) ; return 0 ; } ``` 这样最终终于是可以做到较为稳定的$80pts$~$95pts$……但是还是没有救。 ## 算法$\#\bold {0x04}$ 算法2 + 链表 出于此，我便去找`—扶苏—`神仙：  然后第二天早上发现昨晚他经历艰难的奋斗…感动的个我/dk  但是..!   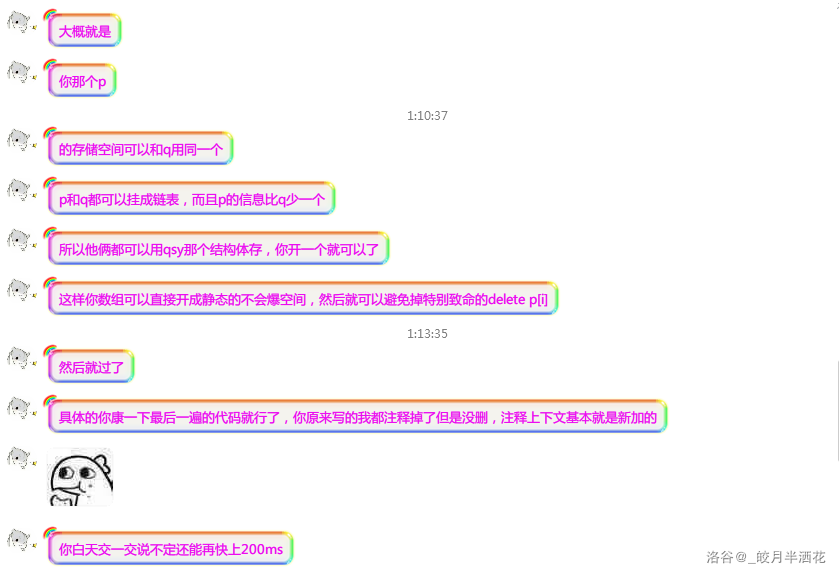很有道理的亚子！于是就是最后代码: ```cpp #include <bits/stdc++.h> #define il inline #define to(k) E[k].to #define next(k) E[k].next #define rg register #define MAXN 1000017 using namespace std ; struct Edge{ int to, next ; }E[MAXN] ; int N, M, cnt ; int head[MAXN], Id[MAXN], kk[MAXN] ; int dep[MAXN], dfn[MAXN], sz[MAXN], buc[MAXN], v[MAXN] ; struct qsy{ int x, id, next ; bool sg ; }; //; int *p[MAXN] ; qsy *q[MAXN] ; qsy pq[MAXN << 1]; int pd[MAXN] ; int pcnt ; il int qr(){ rg char c = getchar() ; rg int res = 0 ; while (!isdigit(c)) c = getchar() ; while (isdigit(c)) res = (res << 1) + (res << 3) + c - 48, c = getchar() ; return res ; } void dfs(const int & u){ sz[u] = 1, dfn[++ cnt] = u, Id[u] = cnt ; for (rg int k = head[u] ; k ; k = next(k)) dep[to(k)] = dep[u] + 1, dfs(to(k)), sz[u] += sz[to(k)] ; } void do_do(const int &u){ buc[++ cnt] = u ; for (rg int i = pd[u]; i; i = pq[i].id) { int x = pq[i].x; v[x] = (cnt > kk[x]) ? buc[cnt - kk[x]] : 0; } // for (rg int i = 1 ; i <= p[u][0]; ++ i) // v[p[u][i]] = (cnt > kk[p[u][i]]) ? buc[cnt - kk[p[u][i]]] : 0 ; for (rg int k = head[u] ; k ; k = next(k)) do_do(to(k)) ; buc[cnt --] = head[u] = 0 ; } int main(){ N = qr(), M = qr() ; rg int u, op ; dep[1] = 1 ; for (rg int i = 2, j ; i <= N ; ++ i) j = qr(), to(++ cnt) = i, next(cnt) = head[j], head[j] = cnt ; cnt = 0, dfs(1) ; for (rg int i = 1 ; i <= M ; ++ i) v[i] = qr(), kk[i] = qr(), buc[v[i]] ++ ; // for (rg int i = 1 ; i <= N ; ++ i) // p[i] = new int[buc[i] + 1], p[i][0] = buc[i] = 0 ; memset(buc, 0, sizeof buc); for (rg int i = 1 ; i <= M ; ++ i) pq[++ pcnt].x = i, pq[pcnt].id = pd[v[i]], pd[v[i]] = pcnt, v[i] = 0 ; // p[v[i]][++ p[v[i]][0]] = i, v[i] = 0 ; cnt = 0, do_do(1) ; // for (rg int i = 1 ; i <= N ; ++ i) delete p[i] ; for (rg int i = 1 ; i <= M ; ++ i) buc[Id[v[i]]] ++, buc[Id[v[i]] + sz[v[i]] - 1] ++ ; pcnt = 0, memset(pd, 0, sizeof pd), memset(buc, 0, sizeof buc) ; // for (rg int i = 0 ; i <= N ; ++ i) // q[i] = new qsy[buc[i] + 1], q[i][0].x = buc[i] = 0 ; for (rg int i = 1, j ; i <= M ; ++ i) { if (!v[i]) continue ; u = Id[v[i]], j = dep[v[i]] + kk[i], op = u + sz[v[i]] - 1 ; pq[++ pcnt] = (qsy){j, i, pd[u], 0}, pd[u] = pcnt ; pq[++ pcnt] = (qsy){j, i, pd[op], 1}, pd[op] = pcnt ; // q[u][++ q[u][0].x] = (qsy){j, i, 0}, q[op][++ q[op][0].x] = (qsy){j, i, 1} ; } for (rg int i = 1 ; i <= N ; ++ i){ buc[dep[dfn[i]]] ++ ; for (rg int j = pd[i]; j; j = pq[j].next) head[pq[j].id] += pq[j].sg ? buc[pq[j].x] : -buc[pq[j].x]; // for (rg int j = 1 ; j <= q[i][0].x ; ++ j) // head[q[i][j].id] += q[i][j].sg ? buc[q[i][j].x] : -buc[q[i][j].x] ; } for (rg int i = 1 ; i <= M ; ++ i) printf("%d ", head[i] > 0 ? head[i] - 1 : head[i]) ; return 0 ; } ``` 可以通过本题。 ## 后记 * ⑧说别的了，zay天下第一！ * fread是真的浪费青春……好烦啊。 * 如果出题人当时就把空间或者时间开大一倍的话，Luogu说不定可以少浪费一堆评测资源，%￥&@#￥%&。 * 祝自己csp rp++，祝zay csp rp++！ 之后的事情：