Splay处理区间操作——翻转操作(Reverse)
皎月半洒花
2018-04-26 11:55:50
嗯呐……我发现本蒟做这种题总会被卡……并且总是被一些奇奇怪怪的东西卡死……呃不是算法,是打代码时不细心,导致调试了好长时间 ORZ。
那么,Splay 的基础操作[戳这里](https://www.luogu.org/blog/pks-LOVING/more-senior-data-structure-te-bie-qian-di-qian-tan-splay)。
那么对于区间反转这种操作,我们由于原数列的顺序已经给定,所以不能按照权值排序,所以选择按照点的编号建立一棵二叉搜索树。
诶,所以啊,不用一个个 `insert` 编号,我们只需要进行一下递归建树即可——建树可以仿照线段树的建树 qwq。
那么就类似这样:
```cpp
struct Splay_tree{
int f,sub_size,cnt,value,tag;
int son[2];
}s[MAXN];
inline void update(int x){
if(x){
s[x].sub_size=s[x].cnt;
if(s[x].son[0])s[x].sub_size+=s[s[x].son[0]].sub_size;
if(s[x].son[1])s[x].sub_size+=s[s[x].son[1]].sub_size;
}
}
int build_tree(int l, int r, int fa) {
if(l > r) { return 0; }
int mid = (l + r) >> 1;
int now = ++ wz;
s[now].f=fa;
s[now].son[0]=s[now].son[1]=0;
s[now].cnt++;
s[now].value=original[mid];
s[now].sub_size++;
s[now].son[0] = build_tree(l, mid - 1, now);
s[now].son[1] = build_tree(mid + 1, r, now);
update(now);
return now;
}
```
emmmm 码风还算是中规中矩吧。
那么我们现在已经有一棵编号树了(并且由于递归建树,一开始是平衡的),我们要对它进行区间翻转操作。那么实际上我们可以发现,在反转区间 $l\sim r$ 的时候,我们可以考虑利用 Splay 的性质,将 $l-1$ 翻转至根节点,再将 $r+1$ 翻转至根节点的右儿子,类似这样:
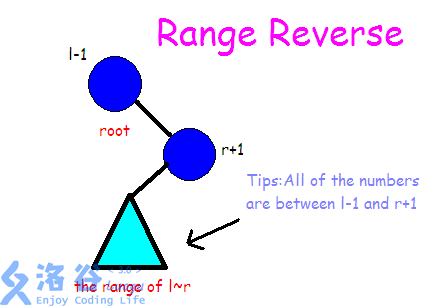
emmm 本蒟蒻用英文作图只是因为会使风格更简约 $qwq$。
但在这里还是需要注意,我们为了方便,在 $1$ 号节点之前和 $n$ 号节点之后又加了两个节点并赋值为 $\rm -INF$ 和 $\rm INF$,作为虚点,既满足二叉搜索树的性质,又可以让我们在翻转 $1\sim n$ 时不会 GG。
那么实际上,在我们把当前区间确定下来之后,我们就要开始进行反转操作。而对于反转操作,我们可以不断替换子节点的左右子树达到此目的。
比如对于 $1\sim 5$ 这个序列,我们反转 $2\sim 4$ 这个区间,过程就是这样:
首先建树,在这里用一个可行的树来举个栗子:
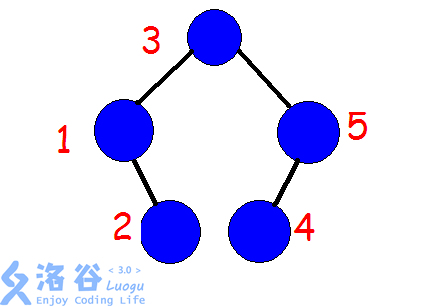
那么实际上我们如果反转 $2\sim 4$ 那么我们需要先将 $1$ 和 $5$ 旋转上去,类似这样:
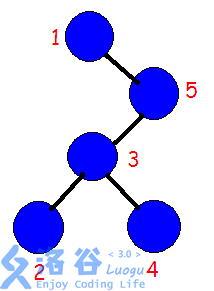
那么实际上我们翻转两个子树就相当于反转 $2\sim 4$ qwq。
但在这个地方我们可以考虑打个标记,标记的存在就只在于记录现在对于当前节点应不应该翻转两个子树。
$\color{gold}Talk$ $is$ $\color{silver}{cheap}$ $,\color{gold}show$ $you$ $the$ $\color{silver}{code}$ :
```cpp
inline void pushdown(int x){
if(x&&s[x].tag){
s[s[x].son[1]].tag^=1;
s[s[x].son[0]].tag^=1;
swap(s[x].son[1],s[x].son[0]);
s[x].tag=0;
}
}
inline int find(int x){
int now=root;
while(1)
{
pushdown(now);
if(x<=s[s[now].son[0]].sub_size){
now=s[now].son[0];
}
else {
x-=s[s[now].son[0] ].sub_size + 1;
if(!x)return now;
now=s[now].son[1];
}
}
}
inline void reverse(int x,int y){
int l=x-1,r=y+1;
l=find(l),r=find(r);
splay(l,0);
splay(r,l);
int pos=s[root].son[1];
pos=s[pos].son[0];
s[pos].tag^=1;//标记最初打在操作区间的根节点上
}
```
然后还有些需要注意的,注释了 qwq。
还有,$copy$ 别人的 $code$ 可耻 qnq。
```cpp
#include<iostream>
using namespace std;
#define MAXN 1000007
#define INF 100000089
struct Splay_tree{
int f,sub_size,cnt,value,tag;
int son[2];
}s[MAXN];
int original[MAXN],root,wz;
inline bool which(int x){
return x==s[s[x].f].son[1];
}
inline void update(int x){
if(x){
s[x].sub_size=s[x].cnt;
if(s[x].son[0])s[x].sub_size+=s[s[x].son[0]].sub_size;
if(s[x].son[1])s[x].sub_size+=s[s[x].son[1]].sub_size;
}
}
inline void pushdown(int x){
if(x&&s[x].tag){
s[s[x].son[1]].tag^=1;
s[s[x].son[0]].tag^=1;
swap(s[x].son[1],s[x].son[0]);
s[x].tag=0;
}
}
inline void rotate(int x){
int fnow=s[x].f,ffnow=s[fnow].f;
pushdown(x),pushdown(fnow);
bool w=which(x);
s[fnow].son[w]=s[x].son[w^1];
s[s[fnow].son[w]].f=fnow;
s[fnow].f=x;
s[x].f=ffnow;
s[x].son[w^1]=fnow;
if(ffnow){
s[ffnow].son[s[ffnow].son[1]==fnow]=x;
}
update(fnow);
}
inline void splay(int x,int goal){
for(int qwq;(qwq=s[x].f)!=goal;rotate(x)){
if(s[qwq].f!=goal){//这个地方特别重要,原因是需要判断的是当前的父亲有没有到目标节点,而如果把“qwq”改成“x”……就会炸
rotate(which(x)==which(qwq)?qwq:x);
}
}
if(goal==0){
root=x;
}
}
int build_tree(int l, int r, int fa) {
if(l > r) { return 0; }
int mid = (l + r) >> 1;
int now = ++ wz;
s[now].f=fa;
s[now].son[0]=s[now].son[1]=0;
s[now].cnt++;
s[now].value=original[mid];
s[now].sub_size++;
s[now].son[0] = build_tree(l, mid - 1, now);
s[now].son[1] = build_tree(mid + 1, r, now);
update(now);
return now;
}
inline int find(int x){
int now=root;
while(1)
{
pushdown(now);
if(x<=s[s[now].son[0]].sub_size){
now=s[now].son[0];
}
else {
x-=s[s[now].son[0] ].sub_size + 1;
if(!x)return now;
now=s[now].son[1];
}
}
}
inline void reverse(int x,int y){
int l=x-1,r=y+1;
l=find(l),r=find(r);
splay(l,0);
splay(r,l);
int pos=s[root].son[1];
pos=s[pos].son[0];
s[pos].tag^=1;
}
inline void dfs(int now){
pushdown(now);
if(s[now].son[0])dfs(s[now].son[0]);
if(s[now].value!=-INF&&s[now].value!=INF){
cout<<s[now].value<<" ";
}
if(s[now].son[1])dfs(s[now].son[1]);
}
int main(){
int n,m,x,y;
cin>>n>>m;
original[1]=-INF,original[n+2]=INF;
for(int i=1;i<=n;i++){
original[i+1]=i;
}
root=build_tree(1,n+2,0);//有一个良好的定义变量习惯很重要……重复定义同一个变量(比如全局的和局部的同名)那么就会发生覆盖。
for(int i=1;i<=m;i++){
cin>>x>>y;
reverse(x+1,y+1);
}
dfs(root);
}
```