题解 P5272 【总而言之神J要去练习篮球】

这题本来是$K\leq 3,Q\leq 5$，然后被mcfx暴打标程后改成$K\leq 10^9,Q\leq 10^3$... 提示：题目名的格式和std某些函数的命名和某个小说很有关系（没错就是我最近看的） #### 算法1 $K=1$，答案为1 可以得到10分的高分 #### 算法2 暴力枚举矩阵并用哈希优化可以做到$O(Q*$矩阵个数$*\log)$，结合算法1可以得到30分的高分，这就是比赛中的最高分数 ----------- 接下来讲正解 先考虑W=H=1。我们的问题就变成了，令$f(X)$为$\sum_{x\in[l1,r1]}\sum_{y\in[l2,r2]}[x \oplus y==X]$($\oplus$是异或)，问$f(X)$有多少种以及它们的出现次数。 打表发现$f(X)$的种数是$O(\log)$的，且每个值都在常数个区间内出现，但是我们需要寻求更直观的方法。假定$l1=l2=0$，这样原问题就被拆成了4个子问题(r1,r2),(l1-1,r2),(l1-1,l2-1),(r1,l2-1) 考虑对于一个$X$和区间$[0,r1],[0,r2]$如何计算$f(X)$。运用数位dp的高超技巧可以发现枚举$X$和$x \oplus y$在某一位分开即可。 ```cpp int cal(int r1,int r2,int x){ int R=r1^r2; int ans=0; for(int i=30;i>=0;--i){ if(((r1>>i&1)||(r2>>i&1))){ int a=r1>>i&1,b=r2>>i&1,c=x>>i&1; int d=(1<<i); if(a&&(b==c))ans+=r2%d+1; if(b&&(a==c))ans+=r1%d+1; if(a&&b&&0==c)ans+=d; } if((x>>i&1)!=(R>>i&1))break; } return ans+(x==R); } ``` 这样我们就知道了为什么$f(X)$只有$O(\log)$个值，这是因为在不同的时候break答案不同。 有了这个之后，我们很快发现每次break的时候其实是对一段区间赋值 ``` r1^r2=101010101100 00(X) 011(X) 0100(X) 01011(X)... ``` 这样问题在$O(\log)$的时间内解决。、 ---------- 再来考虑$W,H$不为$1$的情况，我们要想办法把他转换。 对于两个矩阵，称他们为本质相同当且仅当一个矩阵可以通过整体异或一个数变成另一个矩阵，比如1 0和3 2. 那么对于一个左上角为$(lx,ly)$的矩阵，他的“特征序列”就是它的行列差分后的结果，即$lx\oplus(lx+1),...,(lx+W-2)\oplus(lx+W-1),ly\oplus(ly+1),...,(ly+H-2)\oplus(ly+H-1)$ 于是本质相同当且仅当特征序列相同，这些矩阵只由左上角的元素区分，而这个问题实际上就变成了$W=H=1$的情况，我们只需要对每个等价类计算。 那么，如何得到$lx\oplus(lx+1),...,(lx+W-2)\oplus(lx+W-1),ly\oplus(ly+1),...,(ly+H-2)\oplus(ly+H-1)$的出现规律呢？分行列考虑，一个形如$lx\oplus(lx+1),...,(lx+W-2)\oplus(lx+W-1)$的序列一定是循环出现的。 **结论** 循环节等于$lx\oplus(lx+W-1)$的最高位。 运用高超的二进制技巧，可以发现$lx\oplus(lx+1)$实际上就是$2*lowbit(lx+1)-1$。这个结论考虑进位时发生的事情即可 那么这个值相同，那么就是限制了末尾k位必须相同，则循环节为$2^k$。 考虑$lx\oplus(lx+1),(lx+1)\oplus(lx+2)...$这若干个值，实际上对$lx$的限制就是$lowbit(lx+1),lowbit(lx+2),..,lowbit(lx+W-1)$这些里面的最大值。 可以发现这个值等于$lx\oplus(lx+W-1)$的最高位。 那么要找到一个位置和$(lx,ly)$特征序列一样，其实就是要两边同时满足限制，假设行循环节$2^l$，列循环节是$2^k$，你惊恐地发现问题变成了 “令$f(X)$为$\sum_{x*2^l\in[l1,r1]}\sum_{y*2^k\in[l2,r2]}[x*2^l \oplus y*2^k==X]$($\oplus$是异或)，问$f(X)$有多少种以及它们的出现次数。” 这个东西非常难算，可以用$O(9^K*K*log)$的Dp直接计算最终答案，这就是原先的标算。 **结论** 可以硬点两边循环节都是$\max(2^l,2^k)$。 考虑$lx\oplus ly$的值，如果只有某一边变化，那么值一定会变化。所以它们是互不相关的。 这样问题成功转化为两边都固定末$k$位，对上面求$W=H=1$问题的答案。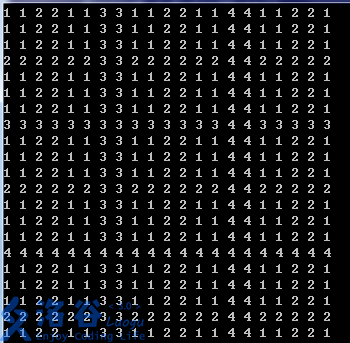可以展示一下这个$k$的样子 ``` #include<bits/stdc++.h> using namespace std; int main(){ int w=2,h=3; for(int i=0;i<=20;++i,puts("")) for(int j=0;j<=20;++j) printf("%d ",max(__lg((i+w-1)^i),__lg((j+h-1)^j))); } ```  接下来我们只需要对每种数字算一下区间即可，留作读者练习。 ```cpp // luogu-judger-enable-o2 // luogu-judger-enable-o2 #include<bits/stdc++.h> using namespace std; typedef long long ll; typedef pair<ll,ll> pii; const int mod=1e9+7; int qpow(int a,int b){ int ans=1; for(;b;b>>=1,a=1ll*a*a%mod) if(b&1)ans=1ll*ans*a%mod; return ans; } namespace orzmcfx{ void add(vector<pii>& ret,ll l,ll r,ll w){ if(!w)return ; ret.push_back(pii(l,w)); ret.push_back(pii(r,-w)); } void getmat(ll r1,ll r2,vector<pii>& ret,int flg){ if(r1<0||r2<0)return ; ll R=r1^r2,ans=0,lstR=0; for(int i=30;i>=0;--i){ int nans=ans; if(((r1>>i&1)||(r2>>i&1))){ int a=r1>>i&1,b=r2>>i&1,c=(R>>i&1)^1; int d=(1<<i); if(a&&(b==c))nans+=r2%d+1; if(b&&(a==c))nans+=r1%d+1; if(a&&b&&0==c)nans+=d; } lstR|=((R>>i&1)<<i); // printf("[%d,%d]",lstR,i); add(ret,lstR^(1ll<<i),(lstR^(1ll<<i))+(1ll<<i),flg*nans); if(((r1>>i&1)||(r2>>i&1))){ int a=r1>>i&1,b=r2>>i&1,c=(R>>i&1); int d=(1<<i); if(a&&(b==c))ans+=r2%d+1; if(b&&(a==c))ans+=r1%d+1; if(a&&b&&0==c)ans+=d; } } add(ret,lstR,lstR+1,flg*(ans+1)); } int CNT=0; vector<pii> st; int cal(ll lx,ll rx,ll ly,ll ry,int K,int A){ vector<pii> ret; if(lx>rx||ly>ry)return 0; getmat(rx,ry,ret,1); getmat(lx-1,ry,ret,-1); getmat(rx,ly-1,ret,-1); getmat(lx-1,ly-1,ret,1); sort(ret.begin(),ret.end()); ll sum=0,ans=0; for(int i=0;i<ret.size();++i){ sum+=ret[i].second; if(sum&&i+1<ret.size()&&ret[i+1].first-ret[i].first){ CNT++; st.push_back(pii(sum,1ll*(ret[i+1].first-ret[i].first+mod)*A%mod)); // st[sum]=(st[sum]+1ll*(ret[i+1].first-ret[i].first)*A)%mod; // printf("[%d,%d,%lld]",ret[i].first,ret[i+1].first-1,sum); } } return ans; } } struct data{ ll dcnt,hl,hr,hw; data(){} data(ll dcnt,ll hl,ll hr,ll hw): dcnt(dcnt),hl(hl),hr(hr),hw(hw){} void print(){ printf("[%lld,%lld,%lld,%lld]\n",dcnt,hl,hr,hw); } }; ll hachimansol(ll lx,ll rx,ll ly,ll ry,ll sx,ll llx,ll lrx,ll sy,ll lly,ll lry,int K){ vector<data> va,vb; if(llx>lrx||lly>lry)return 0; // printf("hachimansol:[%lld,%lld,%lld]",llx,lrx,sx); // printf("[%lld,%lld,%lld]\n",lly,lry,sy); auto npb=[&](ll lx,ll rx,ll liml,ll limr,ll step,ll hw,vector<data>& ret){ ll L=max(liml,lx%step),R=min(rx%step,limr); auto pb=[&](ll l,ll r,ll hl,ll hr,ll hw){ if(l>r||hl>hr)return ; ret.push_back(data(r-l+1,hl,hr,hw)); }; if(L<=R){ pb(liml,L-1,lx/step+1,rx/step,hw); pb(L,R,lx/step,rx/step,hw); pb(R+1,limr,lx/step,rx/step-1,hw); } else { pb(max(liml,R+1),min(limr,L-1),lx/step+1,rx/step-1,hw); pb(liml,R,lx/step+1,rx/step,hw); pb(L,limr,lx/step,rx/step-1,hw); } }; npb(lx,rx,llx,lrx,1ll<<sx,sx,va); npb(ly,ry,lly,lry,1ll<<sy,sy,vb); ll ans=0; auto ball=[&](vector<data>& A,vector<data>& B){ for(auto a:A) for(auto b:B) orzmcfx::cal(a.hl,a.hr,b.hl,b.hr,K,1ll*a.dcnt*b.dcnt%mod); }; ball(va,vb); // printf("ans=[%lld]\n",ans); return ans; } int yukinonsol(ll lx,ll rx,ll ly,ll ry,ll w,ll h,ll K){ rx=rx-w+1,ry=ry-h+1; // printf("[%lld,%lld,%lld,%lld]\n",lx,rx,ly,ry); if(w==1&&h==1)return orzmcfx::cal(lx,rx,ly,ry,K,1); ll t=1,c=0,ans=0; while(t<w||t<h)t<<=1,c++; ans+=hachimansol(lx,rx,ly,ry,c,0,t-w,c,0,t-h,K); // printf("[%lld,%lld]",t,c); for(;c<=30;t<<=1,c++){ ans+=hachimansol(lx,rx,ly,ry,c+1,t-w+1,t-1,c+1,0,t*2-h,K); ans+=hachimansol(lx,rx,ly,ry,c+1,0,t-w,c+1,t-h+1,t-1,K); ans+=hachimansol(lx,rx,ly,ry,c+1,t,t*2-w,c+1,t-h+1,t-1,K); } return ans%mod; } int main(){ // freopen("in.txt","r",stdin); // freopen("std.txt","w",stdout); int Q; scanf("%d",&Q); while(Q--){ ll lx,rx,ly,ry,W,H,K; scanf("%lld%lld%lld%lld%lld%lld%lld",&lx,&rx,&ly,&ry,&W,&H,&K); orzmcfx::CNT=0; int ans=0; orzmcfx::st.clear(); yukinonsol(lx,rx,ly,ry,W,H,K); auto v=orzmcfx::st; // fprintf(stdout,"[%d]",v.size()); sort(v.begin(),v.end()); int lst=0; for(int i=0;i<v.size();++i){ if(i==0||v[i].first!=v[i-1].first)lst=qpow(v[i].first,K); ans=(ans+1ll*lst*v[i].second)%mod; } ans=1ll*ans*qpow(1ll*(rx-lx+1-W+1)*(ry-ly+1-H+1)%mod,mod-1-K)%mod; printf("%d\n",ans); // fprintf(stderr,"[%d]\n",orzmcfx::CNT); } } ```