题解 P1014 【Cantor表】

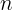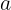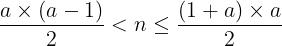
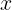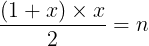
虽然说这道题是考**模拟**.但是为啥感觉很多人真的都在写模拟.... 这道题应该是属于那种给个数据那台计算器都能手打出结论的题哈. 数据小了都不用计算器都能在初中数学范围之内吧。 很明显就是O(1)复杂度(~~这里忽略系统开根的复杂度~~)，求出Z形侧过来的三角形的行数 然后O(1)复杂度(~~又一次忽略系统乘法的复杂度~~)，算出结果。 以下是公式以及简要的解释 已知数据是第个。 明显Z形画出来的三角，从左上到右下的行数是从1开始公差为1的**等差数列**。所以利用**求和公式**，设**行数**为的话则有：  因此我们 设使得  根据建立起的函数的**递增性**，可知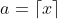 所以通过**求根公式**求出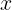然后**向上取整**就可以在O(1)的时间复杂度求出行数了。 ## Which is 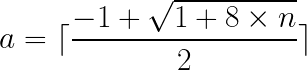 接下来，还要求出所在当行的具体位置，这个就很容易了，只需要知道 到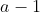那一行总共有多少个：明显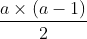个 ### 所以要求的也就是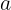那一行的第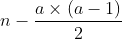个。 接下来是一个对于知道**行数+第几个**的Cantor形式求法： 对于第a行，中所有个体，都有（“/”左边）+（“/”右边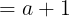） 同时 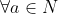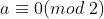， ### 结果是： <u>(\_第几个\_ )/(a+1- \_第几个\_ )</u> ### <u>而剩下的则“/”**两边相反**即好。</u> 以上就是O(1)（~~其实应该没比二分快多少，相当于让系统做了二分而已~~）解决此题的详解。既然是数学推算，代码就不贴了，没啥意思。