[NOIP2014 提高组] 寻找道路

NOIP2014 提高组 D2T2

在有向图 $G$ 中，每条边的长度均为 $1$，现给定起点和终点，请你在图中找一条从起点到终点的路径，该路径满足以下条件： 1. 路径上的所有点的出边所指向的点都直接或间接与终点连通。 2. 在满足条件 $1$ 的情况下使路径最短。 注意：图 $G$ 中可能存在重边和自环，题目保证终点没有出边。 请你输出符合条件的路径的长度。

第一行有两个用一个空格隔开的整数 $n$ 和 $m$，表示图有 $n$ 个点和 $m$ 条边。 接下来的 $m$ 行每行 $2$ 个整数 $x,y$，之间用一个空格隔开，表示有一条边从点 $x$ 指向点 $y$。 最后一行有两个用一个空格隔开的整数 $s,t$，表示起点为 $s$，终点为 $t$。

输出只有一行，包含一个整数，表示满足题目描述的最短路径的长度。如果这样的路径不存在，输出 $-1$。

3 2
1 2
2 1
1 3

-1

6 6
1 2
1 3
2 6
2 5  
4 5
3 4
1 5

3

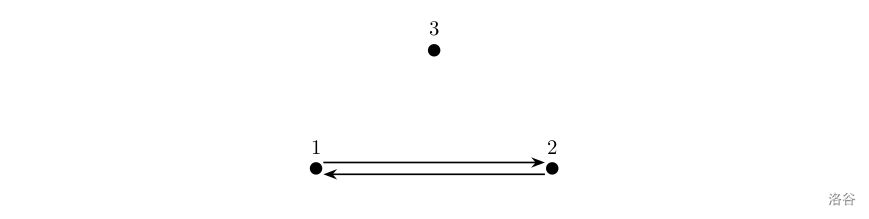
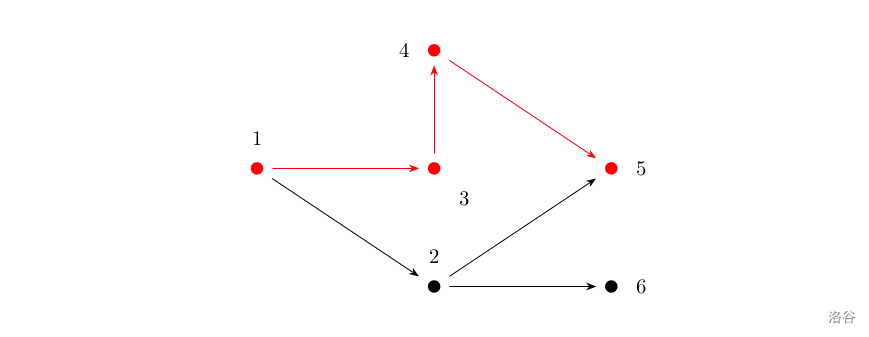
**样例 1 解释**  如上图所示，箭头表示有向道路，圆点表示城市。起点 $1$ 与终点 $3$ 不连通，所以满足题目描述的路径不存在，故输出 $-1$。 **样例 2 解释**  如上图所示，满足条件的路径为 $1\to 3\to 4\to 5$。注意点 $2$ 不能在答案路径中，因为点 $2$ 连了一条边到点 $6$，而点 $6$ 不与终点 $5$ 连通。 **数据范围及约定** - 对于 $30\%$ 的数据，$0<n\le10$，$0<m\le 20$。 - 对于 $60\%$ 的数据，$0<n\le100$，$0<m\le 2000$。 - 对于 $100\%$ 的数据，$0<n\le 10^4$，$0<m\le 2\times 10^5$，$0<x,y,s,t\le n,x,s\ne t$。