[BJOI2019] 光线
题目描述
当一束光打到一层玻璃上时,有一定比例的光会穿过这层玻璃,一定比例的光会被反射回去,剩下的光被玻璃吸收。
设对于任意 $x$,有 $x \times a_i\%$ 单位的光会穿过它,有 $x \times b_i\%$ 的会被反射回去。
现在 $n$ 层玻璃叠在一起,有 $1$ 单位的光打到第 $1$ 层玻璃上,那么有多少单位的光能穿过**所有** $n$ 层玻璃呢?
输入输出格式
输入格式
第一行一个正整数 $n$,表示玻璃层数。
接下来 $n$ 行,每行两个非负整数 $a_i,b_i$,表示第 $i$ 层玻璃的透光率和反射率。
输出格式
输出一行一个整数,表示穿透所有玻璃的光对 $10^9 + 7$ 取模的结果。
可以证明,答案一定为有理数。设答案为 $a/b$ ( $a$ 和 $b$ 是互质的正整数),你输出的答案为 $x$,你需要保证 $a\equiv bx \space (\text{mod }10^9 + 7)$。
输入输出样例
输入样例 #1
2
50 20
80 5输出样例 #1
858585865输入样例 #2
3
1 2
3 4
5 6输出样例 #2
843334849说明
**样例1解释:**
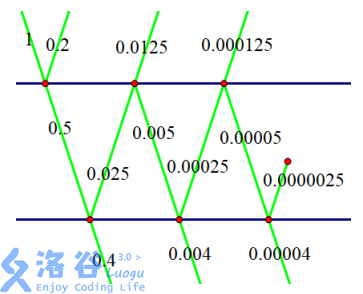
如图,光线从左上角打进来,有 $0.5$ 单位的光穿过第 $1$ 层玻璃,有 $0.2$ 单位的光被反射回去。这 $0.5$ 单位的光有 $0.4$ 单位穿过第 $2$ 层玻璃,有 $0.025$ 单位的光被反射回去。这 $0.025$ 单位的光有 $0.0125$ 单位穿过第 $1$ 层玻璃,有 $0.005$ 单位的光被反射回去。这 $0.005$ 单位的光有 $0.004$ 单位穿过第 $2$ 层玻璃……于是,穿过两层玻璃的光一共有$0.40404... = 40/99$ 单位。在模 $10^9+7$ 意义下等于 $858585865$。
**数据范围:**
对于 $5\%$ 的数据,$n=1$;
对于 $20\%$ 的数据,$n\le 2$;
对于 $30\%$ 的数据,$n\le 3$;
对于 $50\%$ 的数据,$n\le 100$;
对于 $70\%$ 的数据,$n\le 3000$;
对于 $100\%$ 的数据,$n\le 5\times 10^5$,$1\le a_i \le 100$,$0\le b_i \le 99$,$1\le a_i+b_i \le 100$。
每组 $a_i$ 和 $b_i$ 在满足上述限制的整数中随机生成。