Randomizer

题目描述 给定一个包含$n$个点的凸多边形，等概率选取顶点集中大于等于三的子集形成一个新凸多边形，求新凸多边形内部(不包含边界)整点个数的期望值。 输入格式 第一行一个整数$n(3\le n\le 10^5)$; 以下$n$行，第$i+1$行包含两个整数$x_i,y_i(-10^9\le x_i,y_i\le 10^9)$表示一个顶点的坐标，顶点坐标按顺时针给出。 输出格式 一行一个小数，表示整点个数的期望值，精确度$10^{-9}$

Gerald got tired of playing board games with the usual six-sided die, and he bought a toy called Randomizer. It functions as follows. A Randomizer has its own coordinate plane on which a strictly convex polygon is painted, the polygon is called a basic polygon. If you shake a Randomizer, it draws some nondegenerate (i.e. having a non-zero area) convex polygon with vertices at some vertices of the basic polygon. The result of the roll (more precisely, the result of the shaking) is considered to be the number of points with integer coordinates, which were strictly inside (the points on the border are not considered) the selected polygon. Now Gerald is wondering: what is the expected result of shaking the Randomizer? During the shaking the Randomizer considers all the possible non-degenerate convex polygons with vertices at the vertices of the basic polygon. Let's assume that there are $ k $ versions of the polygons. Then the Randomizer chooses each of them with probability .

The first line of the input contains a single integer $ n $ ( $ 3<=n<=100000 $ ) — the number of vertices of the basic polygon. Next $ n $ lines contain the coordinates of the vertices of the basic polygon. The $ i $ -th of these lines contain two integers $ x_{i} $ and $ y_{i} $ ( $ -10^{9}<=x_{i},y_{i}<=10^{9} $ ) — the coordinates of the $ i $ -th vertex of the polygon. The vertices are given in the counter-clockwise order.

Print the sought expected value with absolute or relative error at most $ 10^{-9} $ .

4
0 0
2 0
2 2
0 2

0.2

5
0 0
2 0
2 2
1 3
0 2

0.8125

A polygon is called strictly convex if it is convex and no its vertices lie on the same line. Let's assume that a random variable takes values $ x_{1},...,x_{n} $ with probabilities $ p_{1},...,p_{n} $ , correspondingly. Then the expected value of this variable equals to 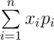.