GCD of Polynomials
题意翻译
题意
构造两个$n$次及以下的多项式$A(x)$和$B(x)$,使得用欧几里得算法计算两个多项式的$gcd$时,算法的运行次数恰好为$n$。
额外限制:多项式的所有系数必须是绝对值小于等于$1$的整数,且最高次项系数应为$1$。
我们认为,算法运行一次,指的是$(A,B)$转移到$(B,A \mod B)$的过程。
输入输出格式
输入
一个整数$n$。
输出
第一行第一个多项式的次数。
第二行这个多项式的系数,从低到高。
第三行和第四行输出第二个多项式。
第一个多项式的次数需大于等于第二个多项式的次数。
无解输出$-1$,多解输出任意。
题目描述
Suppose you have two polynomials 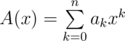 and 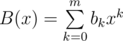. Then polynomial 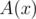 can be uniquely represented in the following way:
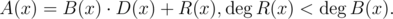This can be done using [long division](https://en.wikipedia.org/wiki/Polynomial_long_division). Here, 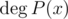 denotes the degree of polynomial $ P(x) $ . 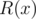 is called the remainder of division of polynomial 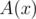 by polynomial 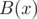, it is also denoted as 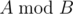.
Since there is a way to divide polynomials with remainder, we can define Euclid's algorithm of finding the greatest common divisor of two polynomials. The algorithm takes two polynomials 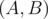. If the polynomial 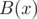 is zero, the result is 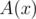, otherwise the result is the value the algorithm returns for pair 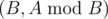. On each step the degree of the second argument decreases, so the algorithm works in finite number of steps. But how large that number could be? You are to answer this question.
You are given an integer $ n $ . You have to build two polynomials with degrees not greater than $ n $ , such that their coefficients are integers not exceeding $ 1 $ by their absolute value, the leading coefficients (ones with the greatest power of $ x $ ) are equal to one, and the described Euclid's algorithm performs exactly $ n $ steps finding their greatest common divisor. Moreover, the degree of the first polynomial should be greater than the degree of the second. By a step of the algorithm we mean the transition from pair 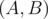 to pair 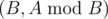.
输入输出格式
输入格式
You are given a single integer $ n $ ( $ 1<=n<=150 $ ) — the number of steps of the algorithm you need to reach.
输出格式
```plain
Print two polynomials in the following format.
```
In the first line print a single integer $ m $ ( $ 0<=m<=n $ ) — the degree of the polynomial.
In the second line print $ m+1 $ integers between $ -1 $ and $ 1 $ — the coefficients of the polynomial, from constant to leading.
The degree of the first polynomial should be greater than the degree of the second polynomial, the leading coefficients should be equal to $ 1 $ . Euclid's algorithm should perform exactly $ n $ steps when called using these polynomials.
If there is no answer for the given $ n $ , print -1.
If there are multiple answer, print any of them.
输入输出样例
输入样例 #1
1
输出样例 #1
1
0 1
0
1
输入样例 #2
2
输出样例 #2
2
-1 0 1
1
0 1
说明
In the second example you can print polynomials $ x^{2}-1 $ and $ x $ . The sequence of transitions is
$ (x^{2}-1,x)→(x,-1)→(-1,0). $ There are two steps in it.