Museums Tour
题意翻译
一个国家有 $n$ 个城市,通过 $m$ 条单向道路相连。有趣的是,在这个国家,每周有 $d$ 天,并且每个城市恰好有一个博物馆。
已知每个博物馆一周的营业情况(开门或关门)和 $m$ 条单向道路,由于道路的设计,每条道路都需要**恰好一个晚上**的时间通过。你需要设计一条旅游路线,使得从首都:$1$ 号城市开始,并且当天是本周的第一天。每天白天,如果当前城市的博物馆**开着门**,旅行者可以进入博物馆参观展览,否则什么也做不了,这一天的晚上,旅行者要么结束行程,要么通过一条道路前往下一个城市。当然,旅行者**可以多次经过一个城市**。
要求让旅行者能够参观的**不同**博物馆数量尽量多(同一个城市的博物馆参观多次仅算一次),请你求出这个最大值。
## 输入输出格式
### 输入格式:
第一行三个整数 $n$、$m$ 和 $d$($1\le n\le 100,000$,$0\le m\le 100,000$,$1\le d\le 50$),分别表示城市的数量,单向道路的数量和一周的天数。
接下来 $m$ 行,每行两个正整数 $u_i$ 和 $v_i$($1\le u_i, v_i\le n$,$u_i\ne v_i$),表示一条从 $u_i$ 到 $v_i$ 的单向道路。
接下来 $n$ 行描述了博物馆的每周日程。第 $i$ 行包含一个长度为 $d$ 的 01 串,如果该串的第 $j$ 个字符为 `1` 则表示 $i$ 号城市上的博物馆在一周的第 $j$ 天开门,为 `0` 则反之。
保证一条道路 $u_i\to v_i$ 不会出现超过两次。
### 输出格式:
输出一个整数:表示在一周的第一天从 $1$ 号城市出发,能够经过的不同博物馆数量的最大值。
题目描述
In the country $ N $ , there are $ n $ cities connected by $ m $ one-way roads. Although this country seems unremarkable, there are two interesting facts about it. At first, a week lasts $ d $ days here. At second, there is exactly one museum in each city of the country $ N $ .
Travel agency "Open museums" is developing a new program for tourists interested in museums. Agency's employees know which days each of the museums is open. The tour should start in the capital — the city number $ 1 $ , and the first day of the tour must be on the first day of a week. Each day a tourist will be in some city, watching the exposition in its museum (in case museum is open today), and by the end of the day, the tour either ends or the tourist goes into another city connected by a road with the current one. The road system of $ N $ is designed in such a way that traveling by a road always takes one night and also all the roads are one-way. It's allowed to visit a city multiple times during the trip.
You should develop such route for the trip that the number of distinct museums, possible to visit during it, is maximum.
输入输出格式
输入格式
The first line contains three integers $ n $ , $ m $ and $ d $ ( $ 1 \leq n \leq 100\,000 $ , $ 0 \leq m \leq 100\,000 $ , $ 1 \leq d \leq 50 $ ), the number of cities, the number of roads and the number of days in a week.
Each of next $ m $ lines contains two integers $ u_i $ and $ v_i $ ( $ 1 \le u_i, v_i \le n $ , $ u_i \ne v_i $ ), denoting a one-way road from the city $ u_i $ to the city $ v_i $ .
The next $ n $ lines contain the museums' schedule. The schedule of the museum located in the $ i $ -th city is described in the $ i $ -th of these lines. Each line consists of exactly $ d $ characters "0" or "1", the $ j $ -th character of the string equals to "1" if the museum is open at the $ j $ -th day of a week, and "0", otherwise.
It's guaranteed that for each pair of cities $ (u, v) $ there exists no more than one road leading from $ u $ to $ v $ .
输出格式
Print a single integer — the maximum number of distinct museums, that it's possible to visit, starting a trip in the first city on the first day of the week.
输入输出样例
输入样例 #1
4 5 3
3 1
1 2
2 4
4 1
2 3
011
110
111
001
输出样例 #1
3
输入样例 #2
3 3 7
1 2
1 3
2 3
1111111
0000000
0111111
输出样例 #2
2
说明
Explanation of the first example 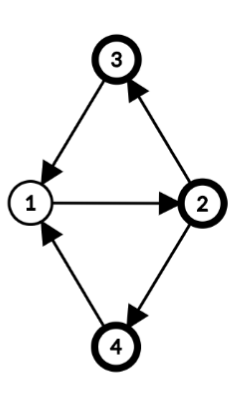The maximum number of distinct museums to visit is $ 3 $ . It's possible to visit $ 3 $ museums, for example, in the way described below.
- Day 1. Now it's the 1st day of a week, and the tourist is in the city $ 1 $ . The museum there is closed. At night the tourist goes to the city number $ 2 $ .
- Day 2. Now it's the 2nd day of a week, and the tourist is in the city $ 2 $ . The museum there is open, and the tourist visits it. At night the tourist goes to the city number $ 4 $ .
- Day 3. Now it's the 3rd day of a week, and the tourist is in the city $ 4 $ . The museum there is open, and the tourist visits it. At night the tourist goes to the city number $ 1 $ .
- Day 4. Now it's the 1st day of a week, and the tourist is in the city $ 1 $ . The museum there is closed. At night the tourist goes to the city number $ 2 $ .
- Day 5. Now it's the 2nd of a week number $ 2 $ , and the tourist is in the city $ 2 $ . The museum there is open, but the tourist has already visited it. At night the tourist goes to the city number $ 3 $ .
- Day 6. Now it's the 3rd day of a week, and the tourist is in the city $ 3 $ . The museum there is open, and the tourist visits it. After this, the tour is over.
Explanation of the second example 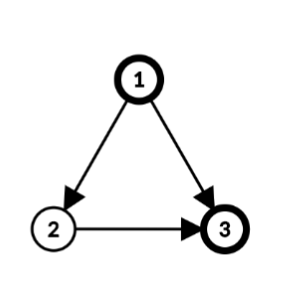The maximum number of distinct museums to visit is $ 2 $ . It's possible to visit $ 2 $ museums, for example, in the way described below.
- Day 1. Now it's the 1st day of a week, and the tourist is in the city $ 1 $ . The museum there is open, and the tourist visits it. At night the tourist goes to the city number $ 2 $ .
- Day 2. Now it's the 2nd day of a week, and the tourist is in the city $ 2 $ . The museum there is closed. At night the tourist goes to the city number $ 3 $ .
- Day 3. Now it's the 3rd day of a week, and the tourist is in the city $ 3 $ . The museum there is open, and the tourist visits it. After this, the tour is over.