Irrational problem
题意翻译
输入p1、p2、p3、p4,输入a和b,求在[a,b]这个区间内有多少个数%p1、%p2、%p3、%p4后还是它本身
Translated by @夜刀神十香ღ
题目描述
Little Petya was given this problem for homework:
You are given function 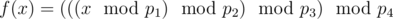 (here 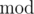 represents the operation of taking the remainder). His task is to count the number of integers $ x $ in range $ [a;b] $ with property $ f(x)=x $ .
It is a pity that Petya forgot the order in which the remainders should be taken and wrote down only 4 numbers. Each of 24 possible orders of taking the remainder has equal probability of being chosen. For example, if Petya has numbers 1, 2, 3, 4 then he can take remainders in that order or first take remainder modulo 4, then modulo 2, 3, 1. There also are 22 other permutations of these numbers that represent orders in which remainder can be taken. In this problem 4 numbers wrote down by Petya will be pairwise distinct.
Now it is impossible for Petya to complete the task given by teacher but just for fun he decided to find the number of integers 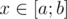 with property that probability that $ f(x)=x $ is not less than $ 31.4159265352718281828459045% $ . In other words, Petya will pick up the number $ x $ if there exist at least $ 7 $ permutations of numbers $ p_{1},p_{2},p_{3},p_{4} $ , for which $ f(x)=x $ .
输入输出格式
输入格式
First line of the input will contain 6 integers, separated by spaces: $ p_{1},p_{2},p_{3},p_{4},a,b $ ( $ 1<=p_{1},p_{2},p_{3},p_{4}<=1000,0<=a<=b<=31415 $ ).
It is guaranteed that numbers $ p_{1},p_{2},p_{3},p_{4} $ will be pairwise distinct.
输出格式
Output the number of integers in the given range that have the given property.
输入输出样例
输入样例 #1
2 7 1 8 2 8
输出样例 #1
0
输入样例 #2
20 30 40 50 0 100
输出样例 #2
20
输入样例 #3
31 41 59 26 17 43
输出样例 #3
9