Axel and Marston in Bitland
题意翻译
## 题目大意
给定一张有向图(可能有自环,保证没有重边),每条边有两种类型,分别为1或者0 从1开始走,要求走过的路径类型成如下方式
0
01
0110
01101001
第$i$个是由第$i -1$个和第$i - 1$个取反拼在后面。 求最长路。
## 输入
第一行两个正整数 $n$,$m$ 分别为有向图点数,边数 接下来$m$行,每行三个整数$u$ ,$v$, $t$ 表示$u$到$v$之间有一条类型为tt的边。
## 输出
输出一个整数,表示最长路 如果最长路严格大于$10^{18}$ ,输出-1.
题目描述
A couple of friends, Axel and Marston are travelling across the country of Bitland. There are $ n $ towns in Bitland, with some pairs of towns connected by one-directional roads. Each road in Bitland is either a pedestrian road or a bike road. There can be multiple roads between any pair of towns, and may even be a road from a town to itself. However, no pair of roads shares the starting and the destination towns along with their types simultaneously.
The friends are now located in the town 1 and are planning the travel route. Axel enjoys walking, while Marston prefers biking. In order to choose a route diverse and equally interesting for both friends, they have agreed upon the following procedure for choosing the road types during the travel:
- The route starts with a pedestrian route.
- Suppose that a beginning of the route is written in a string $ s $ of letters P (pedestrain road) and B (biking road). Then, the string 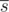 is appended to $ s $ , where 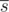 stands for the string $ s $ with each character changed to opposite (that is, all pedestrian roads changed to bike roads, and vice versa).
In the first few steps the route will look as follows: P, PB, PBBP, PBBPBPPB, PBBPBPPBBPPBPBBP, and so on.
After that the friends start travelling from the town 1 via Bitlandian roads, choosing the next road according to the next character of their route type each time. If it is impossible to choose the next road, the friends terminate their travel and fly home instead.
Help the friends to find the longest possible route that can be travelled along roads of Bitland according to the road types choosing procedure described above. If there is such a route with more than $ 10^{18} $ roads in it, print -1 instead.
输入输出格式
输入格式
The first line contains two integers $ n $ and $ m $ ( $ 1<=n<=500 $ , $ 0<=m<=2n^{2} $ ) — the number of towns and roads in Bitland respectively.
Next $ m $ lines describe the roads. $ i $ -th of these lines contains three integers $ v_{i} $ , $ u_{i} $ and $ t_{i} $ ( $ 1<=v_{i},u_{i}<=n $ , $ 0<=t_{i}<=1 $ ), where $ v_{i} $ and $ u_{i} $ denote start and destination towns indices of the $ i $ -th road, and $ t_{i} $ decribes the type of $ i $ -th road (0 for a pedestrian road, 1 for a bike road). It is guaranteed that for each pair of distinct indices $ i $ , $ j $ such that $ 1<=i,j<=m $ , either $ v_{i}≠v_{j} $ , or $ u_{i}≠u_{j} $ , or $ t_{i}≠t_{j} $ holds.
输出格式
If it is possible to find a route with length strictly greater than $ 10^{18} $ , print -1. Otherwise, print the maximum length of a suitable path.
输入输出样例
输入样例 #1
2 2
1 2 0
2 2 1
输出样例 #1
3
输入样例 #2
2 3
1 2 0
2 2 1
2 2 0
输出样例 #2
-1
说明
In the first sample we can obtain a route of length 3 by travelling along the road 1 from town 1 to town 2, and then following the road 2 twice from town 2 to itself.
In the second sample we can obtain an arbitrarily long route by travelling the road 1 first, and then choosing road 2 or 3 depending on the necessary type.