The Intriguing Obsession
题意翻译
齐心协力,我们可以以超乎想象的速度到达任何地方!现在,火炎姐妹 (Fire Sisters) —— 火怜 (Karen) 和月火 (Tsukihi) 正在前往一个她们从未到达的地方——水中的小岛!
有三种不同类型的小岛,方便地,各自涂上了红,蓝,紫三色。每种颜色的小岛各自有 $a,b,c$ 个。
这些小岛之间初始时互相分离。可以在小岛之间架桥,两个小岛间最多架一座桥。
但要满足:任意两个不同的颜色相同的小岛的最短距离要大于等于 $3$(桥的长度为 $1$)。
火炎姐妹已经准备好迎接未知了,但是她们想测试一下你的勇气。你需要计算出不同的架桥方案有多少种,如果有两个小岛之间造桥的方案变了,我们就说这两个造桥的方案不同。答案对 $998244353$ 取模。
#### 输入格式:
一行三个正整数 $a,b,c$($1\le a,b,c\le 5000$),分别表示红、蓝、紫色小岛的个数。
#### 输出格式
输出一个数,表示造桥的方案数,对 $998244353$ 取模。
Translated by @小粉兔
题目描述
— This is not playing but duty as allies of justice, Nii-chan!
— Not allies but justice itself, Onii-chan!
With hands joined, go everywhere at a speed faster than our thoughts! This time, the Fire Sisters — Karen and Tsukihi — is heading for somewhere they've never reached — water-surrounded islands!
There are three clusters of islands, conveniently coloured red, blue and purple. The clusters consist of $ a $ , $ b $ and $ c $ distinct islands respectively.
Bridges have been built between some (possibly all or none) of the islands. A bridge bidirectionally connects two different islands and has length $ 1 $ . For any two islands of the same colour, either they shouldn't be reached from each other through bridges, or the shortest distance between them is at least $ 3 $ , apparently in order to prevent oddities from spreading quickly inside a cluster.
The Fire Sisters are ready for the unknown, but they'd also like to test your courage. And you're here to figure out the number of different ways to build all bridges under the constraints, and give the answer modulo $ 998244353 $ . Two ways are considered different if a pair of islands exist, such that there's a bridge between them in one of them, but not in the other.
输入输出格式
输入格式
The first and only line of input contains three space-separated integers $ a $ , $ b $ and $ c $ ( $ 1<=a,b,c<=5000 $ ) — the number of islands in the red, blue and purple clusters, respectively.
输出格式
Output one line containing an integer — the number of different ways to build bridges, modulo $ 998244353 $ .
输入输出样例
输入样例 #1
1 1 1
输出样例 #1
8
输入样例 #2
1 2 2
输出样例 #2
63
输入样例 #3
1 3 5
输出样例 #3
3264
输入样例 #4
6 2 9
输出样例 #4
813023575
说明
In the first example, there are $ 3 $ bridges that can possibly be built, and no setup of bridges violates the restrictions. Thus the answer is $ 2^{3}=8 $ .
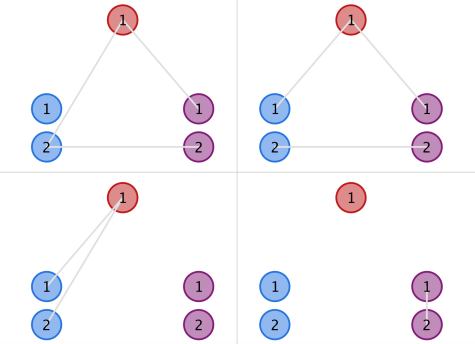
In the second example, the upper two structures in the figure below are instances of valid ones, while the lower two are invalid due to the blue and purple clusters, respectively.