Willem, Chtholly and Seniorious
题意翻译
【题面】
请你写一种奇怪的数据结构,支持:
- $1$ $l$ $r$ $x$ :将$[l,r]$ 区间所有数加上$x$
- $2$ $l$ $r$ $x$ :将$[l,r]$ 区间所有数改成$x$
- $3$ $l$ $r$ $x$ :输出将$[l,r]$ 区间从小到大排序后的第$x$ 个数是的多少(即区间第$x$ 小,数字大小相同算多次,保证 $1\leq$ $x$ $\leq$ $r-l+1$ )
- $4$ $l$ $r$ $x$ $y$ :输出$[l,r]$ 区间每个数字的$x$ 次方的和模$y$ 的值(即($\sum^r_{i=l}a_i^x$ ) $\mod y$ )
【输入格式】
这道题目的输入格式比较特殊,需要选手通过$seed$ 自己生成输入数据。
输入一行四个整数$n,m,seed,v_{max}$ ($1\leq $ $n,m\leq 10^{5}$ ,$0\leq seed \leq 10^{9}+7$ $,1\leq vmax \leq 10^{9} $ )
其中$n$ 表示数列长度,$m$ 表示操作次数,后面两个用于生成输入数据。
数据生成的伪代码如下

其中上面的op指题面中提到的四个操作。
【输出格式】
对于每个操作3和4,输出一行仅一个数。
题目描述
— Willem...
— What's the matter?
— It seems that there's something wrong with Seniorious...
— I'll have a look...

Seniorious is made by linking special talismans in particular order.
After over 500 years, the carillon is now in bad condition, so Willem decides to examine it thoroughly.
Seniorious has $ n $ pieces of talisman. Willem puts them in a line, the $ i $ -th of which is an integer $ a_{i} $ .
In order to maintain it, Willem needs to perform $ m $ operations.
There are four types of operations:
- $ 1\ l\ r\ x $ : For each $ i $ such that $ l<=i<=r $ , assign $ a_{i}+x $ to $ a_{i} $ .
- $ 2\ l\ r\ x $ : For each $ i $ such that $ l<=i<=r $ , assign $ x $ to $ a_{i} $ .
- $ 3\ l\ r\ x $ : Print the $ x $ -th smallest number in the index range $ [l,r] $ , i.e. the element at the $ x $ -th position if all the elements $ a_{i} $ such that $ l<=i<=r $ are taken and sorted into an array of non-decreasing integers. It's guaranteed that $ 1<=x<=r-l+1 $ .
- $ 4\ l\ r\ x\ y $ : Print the sum of the $ x $ -th power of $ a_{i} $ such that $ l<=i<=r $ , modulo $ y $ , i.e. 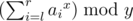.
输入输出格式
输入格式
The only line contains four integers $ n,m,seed,v_{max} $ ( $ 1<=n,m<=10^{5},0<=seed<10^{9}+7,1<=vmax<=10^{9} $ ).
The initial values and operations are generated using following pseudo code:
```
def rnd():
ret = seed
seed = (seed * 7 + 13) mod 1000000007
return ret
for i = 1 to n:
a[i] = (rnd() mod vmax) + 1
for i = 1 to m:
op = (rnd() mod 4) + 1
l = (rnd() mod n) + 1
r = (rnd() mod n) + 1
if (l > r):
swap(l, r)
if (op == 3):
x = (rnd() mod (r - l + 1)) + 1
else:
x = (rnd() mod vmax) + 1
if (op == 4):
y = (rnd() mod vmax) + 1
```
Here $ op $ is the type of the operation mentioned in the legend.
输出格式
For each operation of types $ 3 $ or $ 4 $ , output a line containing the answer.
输入输出样例
输入样例 #1
10 10 7 9
输出样例 #1
2
1
0
3
输入样例 #2
10 10 9 9
输出样例 #2
1
1
3
3
说明
In the first example, the initial array is $ {8,9,7,2,3,1,5,6,4,8} $ .
The operations are:
- $ 2\ 6\ 7\ 9 $
- $ 1\ 3\ 10\ 8 $
- $ 4\ 4\ 6\ 2\ 4 $
- $ 1\ 4\ 5\ 8 $
- $ 2\ 1\ 7\ 1 $
- $ 4\ 7\ 9\ 4\ 4 $
- $ 1\ 2\ 7\ 9 $
- $ 4\ 5\ 8\ 1\ 1 $
- $ 2\ 5\ 7\ 5 $
- $ 4\ 3\ 10\ 8\ 5 $