[NOIP2007 普及组] Hanoi 双塔问题
题目描述
给定 A、B、C 三根足够长的细柱,在 A 柱上放有 $2n$ 个中间有孔的圆盘,共有 $n$ 个不同的尺寸,每个尺寸都有两个相同的圆盘,注意这两个圆盘是不加区分的(下图为 $n=3$ 的情形)。
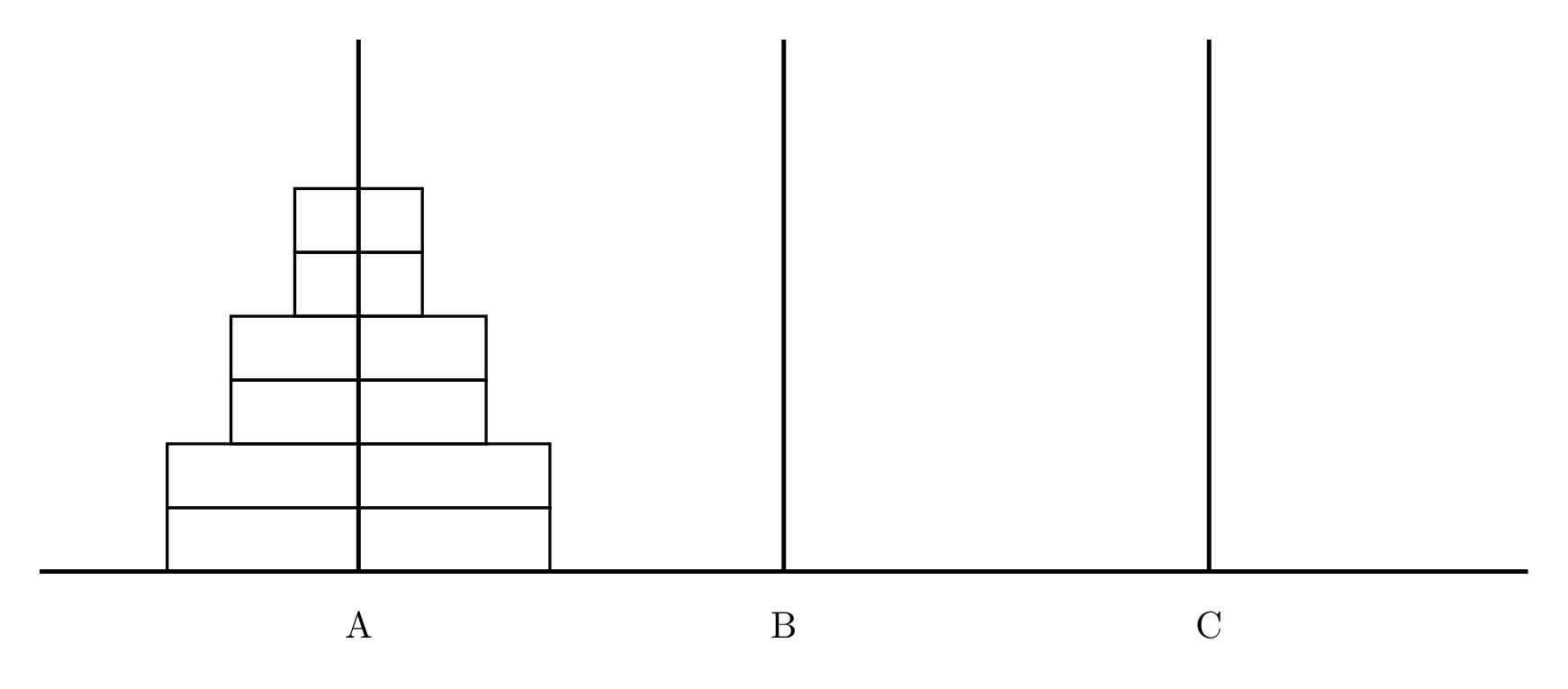
现要将这些圆盘移到 C 柱上,在移动过程中可放在 B 柱上暂存。要求:
1. 每次只能移动一个圆盘;
2. A、B、C 三根细柱上的圆盘都要保持上小下大的顺序。
任务:设 $A_n$ 为 $2n$ 个圆盘完成上述任务所需的最少移动次数,对于输入的 $n$,输出 $A_n$。
输入输出格式
输入格式
一个正整数 $n$,表示在 A 柱上放有 $2n$ 个圆盘。
输出格式
一个正整数, 为完成上述任务所需的最少移动次数 $A_n$。
输入输出样例
输入样例 #1
1输出样例 #1
2输入样例 #2
2输出样例 #2
6说明
**限制**
- 对于 $50\%$ 的数据,$1 \le n \le 25$;
- 对于 $100\%$ 的数据,$1 \le n \le 200$。
**提示**
设法建立 $A_n$ 与 $A_{n-1}$ 的递推关系式。