[WC2018] 通道
题目背景
**滥用本题评测将被封号。**
题目描述
11328 年,C 国的科学家们研发了一种高速传送通道,可以在很短的时间内把居民从通道的一端送往另一端,这些通道都是双向的。
美中不足的是,这种传送通道需要进行大量的维护和检修。经过规划,C 国总统决定在 M 城中新建这种通道,在 M 城中,建立了 $n$ 个传送站和 $3\times(n-1)$ 条传送通道,这些传送通道被分为 $3$ 组,每一组都包含了 $(n-1)$ 条通道。
当任意一组通道运行时,居民都可以通过这组通道从任意一个传送站前往任意的另一个传送站。也就是说,所有的传送站都会被通道所连通。
三组通道按照 $1$、 $2$、 $3$ 的顺序轮流运行,循环反复。在任意一个时刻,都有且只有一组传送通道可以使用。形式化地,在第 $i$ 天中,有且只有第 $((i-1)\bmod 3+1)$ 组通道运行。
C 国著名科学家 Access Globe 正在进行一项社会调查实验:调查两个传送站之间的传送通道使用者的信息。 Access Globe 的计划是这样的:
- 选定两个传送站 $a, b$
- 第一天,他从 $a$ 出发,使用正在运行的这组通道沿最短路径到达 $b$,并调查经过的所有通道上使用者的信息
- 第二天,他从 $b$ 出发,使用正在运行的这组通道沿最短路径到达 $a$,并调查经过的所有通道上使用者的信息
- 第三天,他从 $a$ 出发,使用正在运行的这组通道沿最短路径到达 $b$,并调查经过的所有通道上使用者的信息
Access Globe 知道每一条传输线路在运行时的使用者人数。他希望找出一对 $a, b$,使得在整个实验过程中所有经过的通道的使用者数量之和最大。
Access Globe 希望参加 CCF NOI 2018 冬令营的你帮他解决这个简单的小问题。如果你成功地解决了这个问题, Access Globe 会送你一份小礼物——$100$ 分!
输入输出格式
输入格式
输入文件的第 $1$ 行包含一个正整数 $n$,表示传送站的个数,传送站从 $1$ 到 $n$ 编号;
输入文件的第 $2$ 到第 $n$ 行,每行包含 $3$ 个数 $u,v,w$,表示第一组通道中有一条连接 $u,v$ 的通道,其运行时使用者数量为 $w$ 人;
输入文件的第 $(n+1)$ 到第 $(2n-1)$ 行,每行包含 $3$ 个数 $u,v,w$,表示第二组通道中有一条连接 $u,v$ 的通道,其运行时使用者数量为 $w$ 人;
输入文件的第 $2n$ 到第 $(3n-2)$ 行,每行包含 $3$ 个数 $u,v,w$,表示第三组通道中有一条连接 $u,v$ 的通道,其运行时使用者数量为 $w$ 人。
输出格式
输出文件共 $1$ 行,包含一个整数,表示最大的使用者数量之和。
输入输出样例
输入样例 #1
5
1 2 2
1 3 0
1 4 1
4 5 7
1 2 0
2 3 1
2 4 1
2 5 3
1 5 2
2 3 8
3 4 5
4 5 1输出样例 #1
27说明
【样例$1$说明】
下图为样例中 $M$ 城的传送站和传输线路情况。其中点和虚线交替的线条、虚线条和实线条分别表示第一组、第二组和第三组通道。
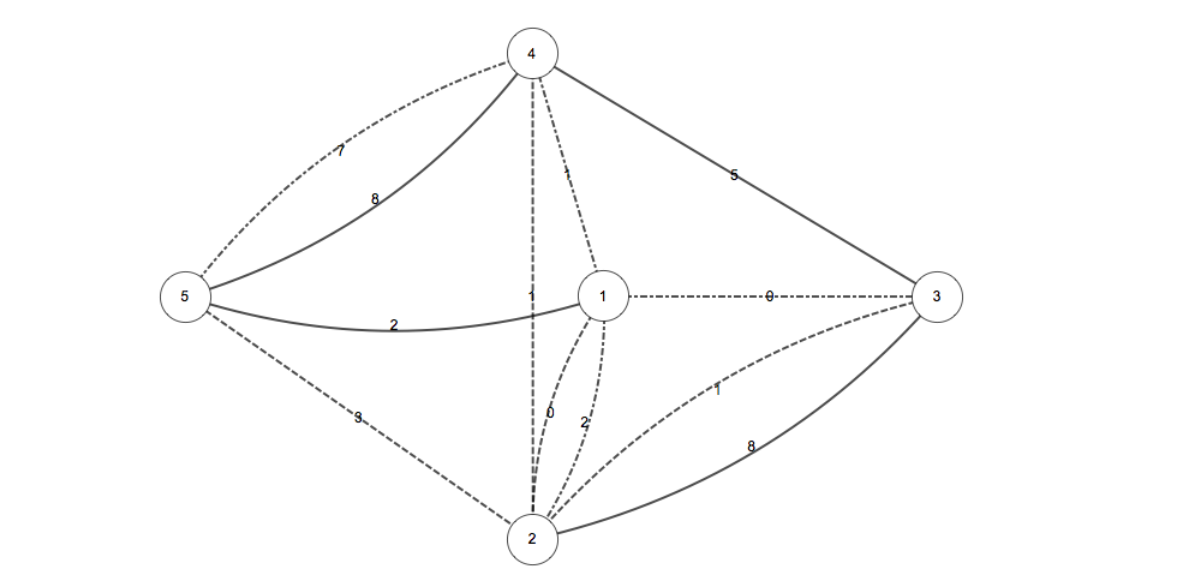
一种可行的方案是选择 $a=2,b=5$,这样的使用者数量之和为 $(3)+(8+5+1)+(2+1+7)=27$。
【子任务】
对于所有数据, $2 \leq n \leq 10^5,0 \leq w \leq 10^{12}$。
特殊性质 $0$:任意两组通道构成完全相同。
特殊性质 $1$:第二组通道和第三组通道构成完全相同。
特殊性质 $2$:对于第二组的每一个传送站,最多只有两个通道可以到达它,且编号为 $x,y$ 的传送站之间通过一条通道直接连接充要条件是 $|x-y|=1$。
特殊性质 $3$:对于第三组的每一个传送站,最多只有两个通道可以到达它。
特殊性质 $4$: $n \leq 3000$。
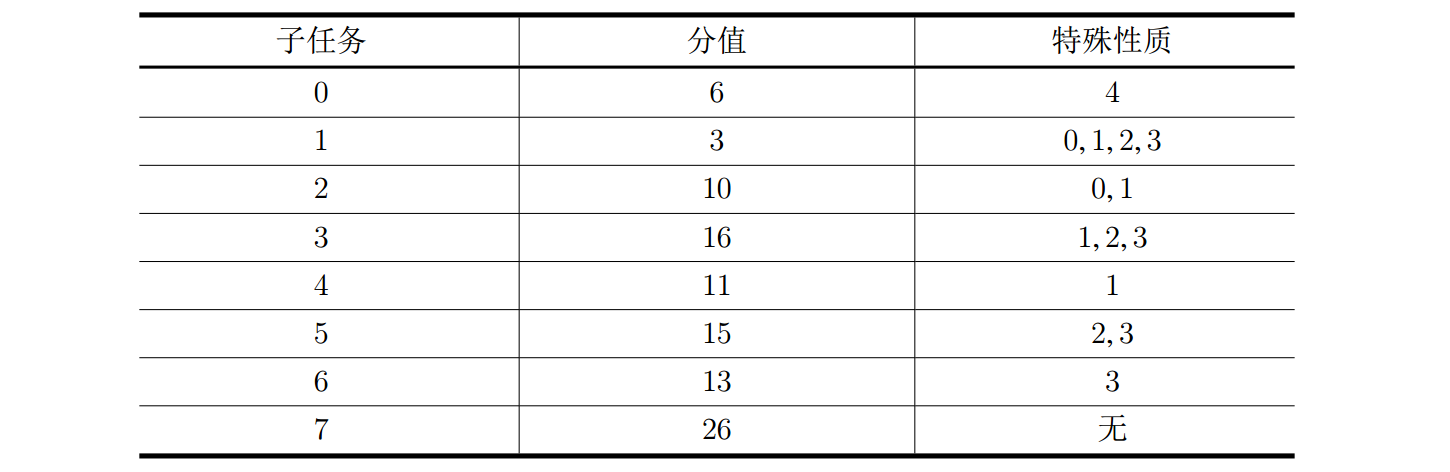
本题共 $31$ 个测试点,每个子任务对应测试点如下:
- 子任务 $0$ 对应测试点 $1-7$;
- 子任务 $1$ 对应测试点 $8$;
- 子任务 $2$ 对应测试点 $9-11$;
- 子任务 $3$ 对应测试点 $12-14$;
- 子任务 $4$ 对应测试点 $15-17$;
- 子任务 $5$ 对应测试点 $18-21$;
- 子任务 $6$ 对应测试点 $22-25$;
- 子任务 $7$ 对应测试点 $26-31$;
【提示】
- 在两组通道中,可能都包含了连接传送站 $x,y$ 的通道,此时我们认为这两条通道是不同的。
- 特殊性质中,A 组通道和 B 组通道的『构成完全相同』是指:如果在 A 组中 $u,v$ 之间存在一条使用人数为 $w$ 的通道,那么在 B 组中 $u,v$ 之间一定也存在一条使用人数为 $w$ 的通道。是否相同与描述方式与描述顺序均无关。即在构成完全相同的两组通道 A 和 B 中,通道输入的顺序不一定相同,每条通道的端点的输入顺序也不一定相同(对于 A、B 组中一条连接 $u,v$ 的使用人数为 $w$ 的通道,一种可能出现的输入为: A 组通道中输入 $u\ v\ w$,而 B 组通道中输入 $v\ u\ w$)。