[HAOI2018] 苹果树
题目背景
HAOI2018 Round2 第一题
题目描述
小 C 在自己家的花园里种了一棵苹果树, 树上每个结点都有恰好两个分支. 经过细心的观察, 小 C 发现每一天这棵树都会生长出一个新的结点.
第一天的时候, 果树会长出一个根结点, 以后每一天, 果树会随机选择一个当前树中没有长出过结点 的分支, 然后在这个分支上长出一个新结点, 新结点与分支所属的结点之间连接上一条边.
小 C 定义一棵果树的不便度为树上两两结点之间的距离之和, 两个结点之间 的距离定义为从一个点走到另一个点的路径经过的边数.
现在他非常好奇, 如果 $N$ 天之后小 G 来他家摘苹果, 这个不便度的期望 $E$ 是多少. 但是小 C 讨厌分数, 所以他只想知道 $E \times N !$ 对 $P$ 取模的结果, 可以证明这是一个整数.
输入输出格式
输入格式
从标准输入中读入数据. 一行两个整数 $N$, $P$ .
输出格式
输出到标准输出中. 输出一个整数表示答案.
输入输出样例
输入样例 #1
3 610745795输出样例 #1
24输入样例 #2
305 1000000007输出样例 #2
865018107说明
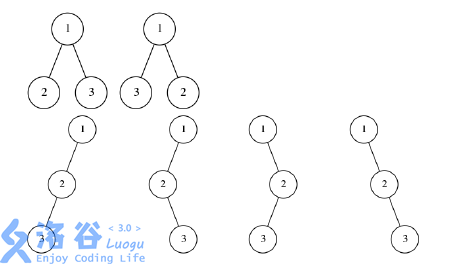
以上是所有 $N = 3$ 时可能的苹果树形态, 其中编号表示这个结点是第几天生
长出来的, 显然每种情况两两结点的距离均为 $4$ .
### 数据范围与约定
| 测试点编号 | $N$ | $P$ |
| :--------: | :--: | :--: |
| $1$ | $\le 10$ | $\le 10^9 + 7$ |
| $2$ | $\le 10$ | $\le 10^9 + 7$ |
| $3$ | $\le 500$ | $\le 10^9 + 7$ |
| $4$ | $\le 500$ | $\le 10^9 + 7$ |
| $5$ | $\le 500$ | $\le 10^9 + 7$ |
| $6$ | $\le 2000$ | $= 10^9 + 7$ |
| $7$ | $\le 2000$ | $= 10^9 + 7$ |
| $8$ | $\le 2000$ | $\le 10^9 + 7$ |
| $9$ | $\le 2000$ | $\le 10^9 + 7$ |
| $10$ | $\le 2000$ | $\le 10^9 + 7$ |