[IOI2007] training 训练路径
题目描述
马克(Mirko)和斯拉夫克(Slavko)正在为克罗地亚举办的每年一次的双人骑车马拉松赛而紧张训练。他们需要选择一条训练路径。
他们国家有$N$个城市和$M$条道路。每条道路连接两个城市。这些道路中恰好有$N-1$条是铺设好的道路,其余道路是未经铺设的土路。幸运的是,每两个城市之间都存在一条由铺设好的道路组成的通路。换句话说,这$N$个城市和$N-1$条铺设好的道路构成一个树状结构。
此外,每个城市最多是$10$条道路的端点。
一条训练路径由某个城市开始,途经一些道路后在原来起始的城市结束。因为马克和斯拉夫克喜欢去看新城市,所以他们制定了一条规则:绝不中途穿越已经去过的城市,并且绝不在相同的道路上骑行两次(不管方向是否相同)。训练路径可以从任何一个城市开始,并且不需要访问所有城市。
显然,坐在后座的骑行者更为轻松,因为坐在前面的可以为他挡风。为此,马克和斯拉夫克在每个城市都要调换位置。为了保证他们的训练强度相同,他们要选择一条具有偶数条道路的路径。
马克和斯拉夫克的竞争者决定在某些未经铺设的土路上设置路障,使得他们两人不可能找到满足上述要求的训练路径。已知在每条土路上设置路障都有一个费用值(一个正整数),并且竞争者不能在铺设好的道路上设置路障。
给定城市和道路网的描述,写一个程序计算出为了使得满足上述要求的训练路径不存在,而需要的设置路障的最小总费用。
输入输出格式
输入格式
输入的第一行包含两个整数$N$和$M$,($2\leq N\leq 1000$,$N-1\leq M\leq5000$),分别表示城市和道路的个数。 接下来的$M$行每行包含$3$个整数$A, B$和$C$($1\leq A\leq N, 1\leq B\leq N, 0\leq C\leq10 000$), 用来描述一条道路。$A$和$B$是不同的整数,表示由这条道路直接相连的两个城市。对于铺设好的道路$C$是$0$;对于土路,$C$是在该条路上设置路障所需的费用值。 每个城市最多是$10$条道路的端点。任意两个城市都不会有多于一条直接相连的道路。
输出格式
输出包含一个整数,表示求出的最小总费用。
输入输出样例
输入样例 #1
5 8
2 1 0
3 2 0
4 3 0
5 4 0
1 3 2
3 5 2
2 4 5
2 5 1 输出样例 #1
5输入样例 #2
9 14
1 2 0
1 3 0
2 3 14
2 6 15
3 4 0
3 5 0
3 6 12
3 7 13
4 6 10
5 6 0
5 7 0
5 8 0
6 9 11
8 9 0 输出样例 #2
48说明
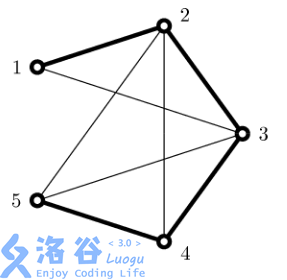
第一个样例中道路与城市的布置。已被铺设好的道路以粗边显示。

共有5种可能的路线。如果边1-3、3-5和2-5被封锁,则两人将会不能使用5种路线的任何一种。封锁这三条边的代价是5。
只封锁两条边,像是2-4和2-5,也是可以的,但这样会导致较高的代价,6。
在前30分的测试数据中,铺设好的道路会形成一条链。