GodFly的寻宝之旅
题目背景
“蒹葭苍苍,白露为霜。所谓伊人,在水一方…”
怀着$a$ $burning$ $desire$,$GodFly$开启了他追寻学妹之路。
题目描述
我们把校园抽象成一个具有$n$个点的无向连通图,其中的$n$个结点分别编号为$1,2,3,...,n$。把$GodFly$经过的结点表示为一个路径集合$A=\left\{a_1,a_2,a_3,...,a_m\right\}$,表示他依次经过了编号为$a_1$、$a_2$、…、$a_m$的结点,由于集合的元素具有互异性,这意味着$GodFly$无法重复经过同一个结点。
$GodFly$现在要从第$1$个结点走到第$n$个结点,然而他的腿疾对他造成了许多不便。定义$GodFly$经过了$m$个结点,当前在点$a_m$,且路径集合$A=\left\{a_1,a_2,a_3...,a_{m-1}\right\}$(加入新结点$a_m$前)时,他的总体力耗费为$w_m=(w_{m-1}+a_m*sum(A))$%$2$,其中$w_{m-1}$表示上一个路径集合的体力耗费;且对于集合$A$,$sum(A)=a_1+a_2+...+a_{m-1}$。
对于$w=0$的情况,我们称$GodFly$处于“滑基态”,否则对于$w=1$的情况,我们称$GodFly$处于“对偶态”。现在$GodFly$想要知道,他走到$n$结点后处于滑基态或对偶态的方案数,由于这个数可能很大,你只需要输出它对$19260817$取膜(模)的结果;注意两个方案是不同的,当且仅当它们有至少一条经过的边不同,而非路径集合不同。
**注意:T3压缩包内第一个数据有误,以题面的样例为准。**
输入输出格式
输入格式
第一行,两个数$n$,$k$,分别表示点数和边数;
接下来$k$行,每行两个数$u$、$v$,表示结点$u$与结点$v$之间有一条边。
输入的最后一行为一个数$c$,$c=0$表示求滑基态方案数,$c=1$表示求对偶态方案数。
输出格式
一行,一个数表示方案数,详见题面。
输入输出样例
输入样例 #1
3 3
1 2
2 3
1 3
1输出样例 #1
2说明
**【数据范围】**
对于$30$%的数据,$n<=10$,$k<=45$,无重边及自环;
对于$60$%的数据,$n<=15$,$k<=300$;
对于$80$%的数据,$n<=15$,$k<=100000$;
对于$100$%的数据,$n<=18$,$k<=100000$;
样例数据在**data.zip\fantasy\**中。
**【样例说明】**
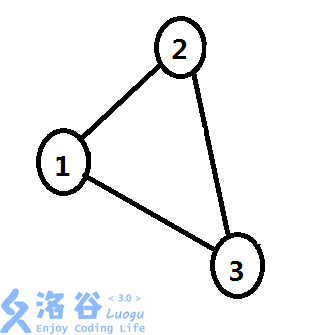
如图,初始时在$1$结点,路径集合为$\left\{1\right\}$,费用为$0$;
若从$1$走到$2$结点再走到$3$结点,到$2$结点时,费用为$(0+2*sum(\left\{1\right\}))$%$2=2*1$%$2=0$,并把$2$加入路径集合,则此时路径集合为$\left\{1,2\right\}$;到$3$结点时,因上一次费用为0,费用为$(0+3*sum(\left\{1,2\right\}))$%$2=3*(1+2)$%$2=1$;
若从$1$结点直接走到$3$结点,则费用为$(0+3*sum(\left\{1\right\}))$%$2=3*1$%$2=1$。
故最终走到$3$结点时费用为$1$的方案数为$2$。
**【提示】**
本题时限$3s$,且可以开启$O_2$优化,不必过分担心卡常数,但请确保算法足够优美。