回忆京都
题目背景
第十五届东方人气投票 音乐部门 106名
第四次国内不知道东方的人对东方原曲的投票调查 51名
回忆京都副歌我tm吹爆,东方文花帖我tm吹爆!
题目描述
射命丸文在取材中发现了一个好玩的东西,叫做组合数。
组合数的定义如下:从$n$个不同元素中,任取$m(m \leq n)$个元素并成一组,叫做从$n$个不同元素中取出$m$个元素的一个组合。所有组合的数量,就是组合数。
组合数的计算公式如下:$C^m_n=\dfrac{n!}{m! \times (n-m)!}$,其中保证$m \leq n$,表示在$n$个元素中选出$m$个元素的组合数。
为了方便理解,举一个例子:在th16.5秘封噩梦日记的第三周目中,每一天的战斗都有$4$个角色两两组合出场,那么很显然就有$C^2_4=6$种组合方式。
关于这方面的更详细解释,请看样例说明。
由于她对新事物都存在着好奇,因此她想要知道$C^m_n$是多少。这对她来说是个很简单的事情,因此她看了一眼就秒了,因此她决定求出下列式子:
$\sum_{i=1}^n \sum_{j=1}^m C^i_j$,其中当$i>j$的时候,钦定$C^i_j$为$0$
她也很快就算出来了,不过对自己的答案不是很充满信心,因此你决定帮助她。然而没事找事的她一下子算了$q$次对于不同的$n,m$的结果,因此这只能劳烦你了。由于你不打算真正地帮助她,你无需把答案对$998244353$取模,也无需对$64123$取模,只要告诉她对$19260817$取模之后的答案即可。
输入输出格式
输入格式
第一行输入一个$q$,表示有$q$次询问。
第二行开始,一共$q$行,每行两个数字$n,m$,意思如题所示。
输出格式
一共$q$行,对于每一个询问,都输出一个答案。
输入输出样例
输入样例 #1
5
2 3
1 4
4 3
2 5
3 5输出样例 #1
10
10
11
35
50说明
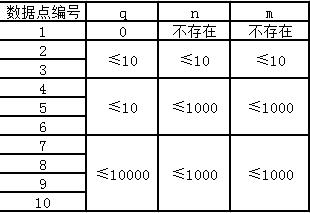
关于组合数的样例说明。
例如有蕾米莉亚 芙兰朵露 圣白莲 丰聪耳神子在这一天组合出场,会有六种情况:
1、蕾米莉亚x芙兰朵露 $\text{\color{white}背德组}$
2、丰聪耳神子x圣白莲 $\text{\color{white}宗教组}$
3、蕾米莉亚x丰聪耳神子
4、芙兰朵露x丰聪耳神子
5、蕾米莉亚x圣白莲
6、芙兰朵露x圣白莲